| Teil Heim
Produktion, Amateur Funkamateur Modellflugzeuge, Raketen- Nützlich, unterhaltsam |
Stealth - Master
Elektronik Physik der Technik Erfindung |
Raum Geheimnis
Erde Mysteries Secrets of the Ocean List Kartenausschnitt |
|
| Verwendung des Materials ist für die Referenz (für Websites - Hyperlinks) zulässig | |||
Navigation: => |
Startseite / Physik / Experiment / |
|
Auf die Möglichkeit mechanisches System von beweglichen
Aufgrund interner Kräfte
![]()
Hinterlassen Sie einen Kommentar

Der Autor kommt mit den neuen Gesetzen und in jedem Fall
Es versucht nicht , den Strom zu unterbrechen.
Ist es möglich, das geschlossene mechanische System zu bewegen, die nicht auf die durch äußere Kräfte gehandelt wird?
Es gibt einen Satz über die Anzahl der Bewegungen:
Die zeitliche Ableitung des Vektors Menge der Bewegung eines Systems ist der Hauptvektor aller äußeren Kräfte auf das System einwirken.
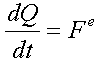
Dieser Satz impliziert mehrere Konsequenzen:
- Innere Kräfte nicht direkt auf die Änderung in der Menge der Bewegung des Systems beeinflussen.
- Wenn der Hauptvektor aller äußeren Kräfte auf das System einwirken Null ist, bleibt die Anzahl der Vektor - Material Bewegung des Systems konstant in Betrag und Richtung.
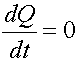
- Wenn die Projektion des resultierenden Vektors der äußeren Kräfte auf das System durch eine bestimmte feste Achse angelegt wird , gleich Null ist , dann die Projektion der Menge der Bewegung des Systems bleibt auf dieser Achse konstant.
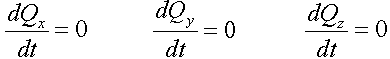
Folgen (2.3), in der Tat, die so genannte Gesetz der Impulserhaltung.
Für ein geschlossenes System, das heißt, führt das System erfahren keine äußeren Einflüsse, oder in dem Fall, wo der geometrische Nettokraft auf das System der äußeren Kräfte gleich Null ist, gibt es ein Gesetz der Impulserhaltung.
Die Anzahl der Bewegungs Teile des Systems (beispielsweise unter dem Einfluß der Schnittkräfte) kann variieren, aber so , dass die Menge
![]() konstant bleibt.
konstant bleibt.
Das Gesetz der Impulserhaltung nicht gebrochen werden kann. Unmöglich!
Und es kann nicht umgangen werden.
Und wenn Sie es nicht verwenden, um das Problem zu lösen, auf den ersten Blick gegen das Gesetz?
Ich bringe das folgende Schema des Arguments , um Ihre Aufmerksamkeit:
In Figur 1 gezeigt bewegenden Körpers kann nicht ohne den Prozess in dem anderen Körper erfolgen.
Da der Betrag der Bewegung des Körpers in der Projektion auf die Koordinatenachsen, kontinuierlich variiert und von Null verschieden ist.
Abb.1
Miteinander verbundene und untrennbare nicht dehnbaren Körper-Verbindung kann, wie in 2 gezeigt ist, bewegt werden.
Mit dieser Bewegung wird der Körper in einem Kreis, dessen Radius bewegen, ist umgekehrt proportional zu ihren Massen.
Diese - eine Folge des Gesetzes der Erhaltung des Impulses.
In diesem Fall ist der Gesamtimpuls des Systems Null ist.
Abb.2
Hier ist, wie es in dem Fall von zwei "echte" Objekte (Abbildung 3) aussehen würde.
Wir nennen eine von ihnen "Körper", und eine andere - "Arbeitsfluid" oder "Arbeitssubstanz".
Figur 3
Wenn die Relativbewegung in (um) das Gehäuse teilnehmen zwei Arbeitskörper (mit der gleichen Masse und der Geschwindigkeit der relativen Verschiebung) (Figur 4), in einem solchen Fall erhält der Körper eine Drehbewegung.
In diesem Fall ist der Gesamtimpuls der beiden Arbeitsflüssigkeiten in der Projektion auf die X-Achse Null ist.
Daher ist der Impulskörper, in der Projektion auf der gleichen Achse, so daß es gleich Null ist.
Der Fall, wird eine Hin- und Herbewegung relativ zu dem Zentrum der Masse des gesamten Körpersystem.
den Körper bewegt wird, wird entlang einer Achse werden von der "absoluten" durchgeführt wird, ein Koordinatensystem festgelegt.
In dem Koordinatensystem mit dem Körper verbunden sind, arbeiten, um die Körper in einem Kreis zu bewegen.
In dem festen Koordinatensystem bewegen Arbeitsgremien in einer elliptischen Bahn.
Machen die kinetische Energie der mechanischen Komponenten des Systems aufgrund der Umwandlung von anderen Arten von Energie, die in dem geschlossenen System enthalten ist möglich.
Das heißt, organisieren die Relativbewegungen der Systemkomponenten können auf interne Kräfte zurückzuführen sein.
In diesem Fall ist der Massenmittelpunkt des gesamten Systems wird immer an Ort und Stelle bleiben, das heißt, nicht seine Koordinaten zu ändern (oder einheitlich bewegen).
Abbildung 4
Wir modifizieren das System in Figur 1 gezeigt.
Wir verwenden keine "Punkt" der Körper und gleichmäßig verteilt, zu einem bestimmten Zeitpunkt der Bahn, die Arbeitermassen (Abbildung 5).
Abbildung 5
Mit einer einheitlichen Relativbewegung zwischen "Körper" und den "arbeitenden Massen" in einem Kreis, dessen Radius bewegen, ist umgekehrt proportional zu ihren Massen (Abbildung 6). Unter dem Radius der Bahn der Arbeitermassen müssen den Radius der Bahn des Massenmittelpunkt (CM) der arbeitenden Massen (der rote Punkt in der Figur) zu verstehen.
Figur 6
Hier ist, wie es für einen "echten" Telefonsystem aussehen würde. (Abbildung 7)
7
Ähnlich (Figur 4) kann in das System aus einer Anzahl von arbeitenden Massen den Drehimpuls zum Ausgleich verwendet werden. (8)
Auch hier ist das Zentrum der Masse des Systems festgelegt.
8
Und was passiert , wenn die Arbeitermassen gleichmäßig sein wird und innig den gesamten Fahrweg füllen? (Abbildung 9) Nichts! Das Zentrum der Masse der arbeitenden Massen fällt mit dem Zentrum der Masse des Körpers. Der Gesamtimpuls der arbeitenden Massen in einer Projektion auf allen Achsen verteilt ist Null. Daher Nullimpuls und das Gehäuse.
Die Zentren der Masse von Systemkomponenten sind nicht relativ zueinander bewegt werden. Systemstabilität ist stationär. Zur gleichen Zeit können wir die bewegte Masse des Arbeits erhebliche kinetische Energie passieren.
9
"Interessant" beginnt, wenn wir beginnen, zu einem bestimmten Punkt der Bahn Bewegung der arbeitenden Massen zu stoppen. (Abbildung 10)
Stop - das heißt, in diesem Fall - aufeinanderfolgende "compound" aller elementaren Teilchen der Arbeitsmasse mit dem Gehäuse.
Das heißt, die Partikel der arbeitenden Massen zu einem bestimmten Punkt der Flugbahn durchgängig Geschwindigkeit Körper gewinnen, die relative Bewegungsgeschwindigkeit zu verlieren. Zugleich geht der Rest der arbeitenden Massen zu bewegen, bis alle seine Teilchen nicht die Körpergeschwindigkeit zu erwerben.
Zum Beispiel können einige Flüssigkeit entlang einer geschlossenen Bahn bewegt, beginnen wir plötzlich in einem Behälter zu sammeln, die fest im Gehäuse montiert ist.
10
In animierte Figur bedingte CM der Arbeitermassen ist rot markiert. Green - die Trajektorie der Bewegung des CM in seiner Relativbewegung gegenüber der "Körper".
Bewegen der Radiusvektor des CM der arbeitenden Massen können als die Bewegung eines Pendels mit variabler Masse und variabler Länge betrachtet werden. (In dem Koordinatensystem mit dem Körper verbunden sind.)
Hier und beschlossen, eine interessante Herausforderung dar:
- berechnen, wie Systemkomponenten zu bewegen?
Die Berechnungen haben zu folgendem Ergebnis (Figur 11) geführt.
Nach der Fertigstellung des gesamten Anschlagmasse CM des gesamten Systems Arbeitszyklus ist in Bezug auf seine Anfangsposition verschoben wird. Das System bewegt sich in Übereinstimmung mit dem Gesetz der Impulserhaltung!
Man könnte sagen , anders: Um das Gesetz der Impulserhaltung, Massenmittelpunkt des mechanischen Systems zu implementieren ist erforderlich , sich zu bewegen.
Die erste Berechnung erfolgt auf der Grundlage des Gesetzes der Erhaltung des Impulses gemacht.
Die zweite - mit Hilfe von Lagrange Gleichungen vom Typ II.
Die Ergebnisse sind die gleichen.
Bei der Lösung dieses Problems nicht vollständig internen Zusammenwirken der Systemkomponenten berücksichtigt.
Keine Kollisionen!
Es gibt keine Trägheitskräfte!
Nur die kinetische Energie und der Zustand des Systems.
11
11 hinzugefügt, um die letzte, dritte Stufe - die Reduktion der Zentren des Massenwohnungsbau und die arbeitenden Massen an einer Stelle. Es ist erforderlich, für eine visuelle Darstellung des gesamten Zyklus der Bewegung, mit der Möglichkeit der Wiederholung dieses Zyklus. Die rote Linie in der Figur stellt den Pfad des CM des gesamten Systems, blau - CM-Gehäuse.
Mathematische Berechnungen, beschreibt dieses Phänomen zu erwarten ist, können Sie einen Blick auf die folgende Adresse erfolgen kann: http://varipend.narod.ru
Druckversion
Autor: Sergej Butov
PS Material geschützt.
Erscheinungsdatum 23.12.2006gg




Kommentare
im Auge kommentierte halten , dass der Inhalt und der Ton Ihrer Nachrichten , die Gefühle von echten Menschen verletzen können, Respekt und Toleranz gegenüber seinen Gesprächspartnern, auch wenn Sie Ihr Verhalten in Bezug auf die Meinungsfreiheit und die Anonymität des Internets, ändert ihre Meinung nicht teilen, nicht nur virtuell, sondern realen Welt. Alle Kommentare werden aus dem Index, Spam - Kontrolle versteckt.