Teil Heim Produktion, Amateur Funkamateur Modellflugzeuge, Raketen- Nützlich, unterhaltsam	Stealth - Master Elektronik Physik der Technik Erfindung	Raum Geheimnis Erde Mysteries Secrets of the Ocean List Kartenausschnitt
Verwendung des Materials ist für die Referenz (für Websites - Hyperlinks) zulässig

AUF DER STÖRUNGEN VON WELLEN

Stetsovich VI

Hinterlassen Sie einen Kommentar

Die physikalischen Vorgänge beim Entstehen, die Ausbreitung, Interferenz und Beugung der Schallwellen.

Es wird gezeigt , dass die Energiedichte, die auf die Welle ist proportional der resultierenden Schwingung auf die Amplitude und die Frequenz der Schwingungsquelle und der Interferenz der Wellen ist die Energie die Summe der Energien der austretenden Wellen übertragen wird.

Die moderne Wellentheorie erklärt die sehr umfangreiche Palette in der Natur Welle Prozesse beobachtet. Und dennoch, die Analyse von Interferenzeffekten führt zu Ergebnissen, die mit den Ergebnissen der Wellentheorie unvereinbar sind.
Nach den allgemein anerkannten Vorstellungen, wenn an einem gewissen Punkt in der Beobachtung zweier kohärenter Wellen ausbreiten in der gleichen Richtung hinzugefügt:

Wieder harmonische Schwingung der gleichen Periode wird:

die Amplitude A und der Anfangsphase resultierende Schwingung durch das Vektordiagramm bestimmt (Abbildung 1)

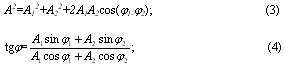
Da die Wellenenergiedichte zu dem Quadrat der Amplitude dieses Bereichs proportional ist, dann ist die Störung der Energie der resultierenden Schwingung ist auf die Summe der Energien der austretenden Welle nicht gleich und variiert von bei am Punkt der maximalen Interferenz bei Interferenzminimum an den Punkten.
Im einfachsten Fall der Gleichheit der Amplituden der störenden Wellen: Die Amplitude der resultierenden Schwingung von Null auf das Minimum zu dem Maximum von 2A variiert und die entsprechende Intensität von 0 bis 4A ^2.

Unterdrückung von Schwingungen in einigen Orten und in anderen gewinnen sie auf eine Transformation der Energieschwankungen nicht in Zusammenhang stehen. Wenn somit das Interferenzproblem reduziert wird, als ob nur zu einer Umverteilung der Leistungsschwankungen und Veränderungen in der Richtung ihrer Übertragung, aber die Energieerhaltungsgesetz ist streng durchgeführt. [1]

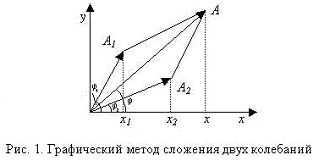
Die Verteilung der Schallwellenenergiedichte entlang der Richtung seiner Ausbreitung in 2 gezeigt ist [2]. Die Figur zeigt , daß im Bereich der Verdickung im Bereich der Unterdruckwellen tragen gleiche Ströme von Energie, so dass die Interferenz von zwei Wellen, und am Interferenzmaximum (dh. A, Figur 3), wenn die Druckamplitude und Geschwindigkeit gebildet werden , und Interferenzminimum an dem Punkt (m. G, 3), wenn die Fläche überlappt , eine Welle der Kondensation mit einer Fläche von rarefaction anderen beiden Abschnitten überlagert Wellen , die die gleiche Energie tragen, die ebenso Vorrichtungen befestigt werden soll. Jedoch an Punkten Interferenzmindestenergie ist nicht festgelegt.

Die Umverteilung von Energie in Bezug auf die maximale Interferenz ist nur möglich, wenn die Störung von ändert sich die Richtung der Wellenenergieübertragung. Berücksichtigung dann einen längeren Weg und eine konstante Geschwindigkeit der Wellenenergieverteilung im Medium könnte die Wellenenergieverteilung im Bereich von Störungen aufgezeichnet werden verlangsamt. Da dies nicht beachtet wird, muss es, dass sich mit einer Geschwindigkeit größer als die Geschwindigkeit der Wellenausbreitung in dem Medium in der Interferenzwelle angenommen werden, Energie übertragen wird, was offensichtlich unrealistisch ist.

In der Ausbreitung von Wellen durch einander übergeben, wird es sich nicht gegenseitig zu beeinflussen. Ähnlich sind die Durchtrittsstellen mit Nullamplitudenschwankungen in der Interferenz (dh. Oh, Abbildung 3) zwei kohärente Wellen breiten sich weiter , ohne Änderungen in dem Maximalpunkt (d. A, Figur 3), es ist die Summe der Amplituden der Wellen ohne Zögern -oder Zeitverzögerungen. Folglich sind die Wellen tragen Energie durch die Punkte Interferenzminimum und keine Umverteilung von Energie in Bezug auf die maximale Interferenz-Nr.
Probleme entstehen, die Interferenz von elektromagnetischen Wellen bei der Erläuterung. Elektromagnetische Welle ist eine Menge von Variablen der elektrischen und magnetischen Felder, die im Raum ausbreiten , und weil, wenn die Überlagerung zweier kohärenter Wellen am Interferenzminimum des elektrischen Feldes Null konstant ist, die Wellenausbreitung auf ohne variablen Felder (E und H) durch den Punkt des Interferenzminimum nicht sein kann . Es ist nicht klar, und dass die Gründe, warum nach der Interferenz minimale Amplitude der elektromagnetischen Welle steigt vorbei.

Wenn die korpuskulare Interpretation des Phänomens der Interferenz elektromagnetischer Wellen kann nicht als Punkt des Interferenzmaximum beobachtet Energieabgabe erläutert, die auf Photonen fallen größer ist als die Energiemenge ist, und es ist nicht klar, wie und wo die verlorene Energie und Impuls, der von Photonen durchgeführt werden, bei der Interferenzminimum und wo sie treten nach ihrer Passage.

Das Wesen des Wellenprozess ist es, die Schwingungsenergie von einem Punkt im Raum zu einem anderen, usw. zu übertragen Was ist der Mechanismus der Energieübertragung durch den Bereich des Raumes, wo Messungen keine Wellen zeigen und dementsprechend die Energieübertragung?

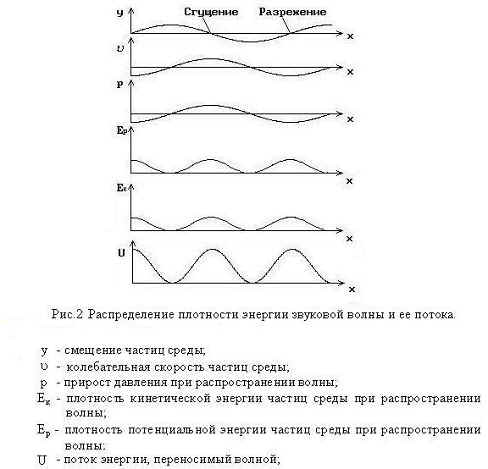
Zur Erklärung dieser Phänomene erscheint es notwendig, im Detail die Prozesse im Falle stattfinden zu betrachten, und die Ausbreitung von Wellen. Da die Grundgesetze der Wellenbewegung gleich sind, werden wir den Fall betrachten, die der einfachste Weg ist, klar zu erklären - Ausbreitung von Schallwellen in einem idealen Gas.

Bei der Analyse der Prozesse in der Ausbreitung von Schallwellen in einem idealen Gas auftritt, gehen wir davon aus, dass:

• die Gasmoleküle die gleiche Masse haben;
• in Kollisionen von Molekülen miteinander - die Wechselwirkung von elastischen, nach den Gesetzen der Kollision von Bällen;
• durch die Bewegung der beiden Moleküle konfrontiert; gleichzeitige Kollision von drei oder mehr Molekülen ist unwahrscheinlich;
• Teilchen durchlaufen nur Frontalkollisionen, die in Richtung der kollidierenden Moleküle, die nur zu einer Veränderung führen und die Richtung ihrer Geschwindigkeiten nicht zu irgendwelchen anderen Winkel zu ändern;
• Moleküle können in der Richtung der Koordinatenachsen x, y, z, und 1/3 der Gesamtanzahl von Molekülen entlang der x - Achse bewegt Hälfte des Bildschirms bewegt sich in einer Richtung bewegen , die die Quelle der Störungen, und die andere Hälfte davon;

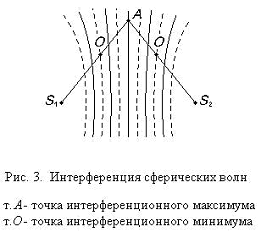
Angenommen , dass eine externe Kraft Bildschirm mit der Geschwindigkeit bewegt , u in der x - Richtung (Figur 4) Achse. Gasmoleküle bewegt sich in Richtung der Bildschirm mit einer Rate von "-U0" in zufälliger Reihenfolge ausgewählt, nach dem Aufprall eine Geschwindigkeit u0 haben + u. In diesem Fall berücksichtigt sie die Tatsache , dass die Temperatur des Mediums und dem gleichen Bildschirm und in dem Prozess der Interaktion eines Moleküls zunächst auf der Oberfläche des Bildschirms adsorbiert wird, und nach einiger Zeit entfernt, in Bezug auf die Geschwindigkeit u0 Bildschirm relativ zu dem externen Beobachter u0 + u. Wenn wir die Wechselwirkung von Molekülen mit einem beweglichen Bildschirm , wie die elastische Kollision von Kugeln, die Geschwindigkeit der Moleküle betrachten wird u0 + 2u alle aufgeführten auf die Formel nur in den Koeffizienten unterscheiden.

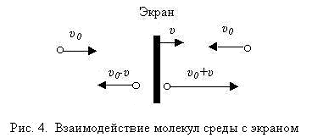
In jedem Fall wird der Impuls und die kinetische Energie der Moleküle erhöht, was zu einer Erhöhung führt, gegenüber dem ungestörten Zustand, innere Energie des Gases.

Auf der gegenüberliegenden Seite des Bildschirms nach einer Kollision mit ihnen die Moleküle Geschwindigkeit reduziert: u0 -u, und die innere Energie des Gases geringer sein wird als die anfängliche, ungestörte Zustand.

Die sich abzeichnende Ressentiment physikalischer Parameter in der Umwelt als Folge der Wechselwirkung zwischen den Teilchen zu dem Gesetz der Impulserhaltung eines geschlossenen Systems nach, mit der Geschwindigkeit c ausbreiten wird, und bewegt sich weg von dem Bildschirm, die Hälfte der Partikel entlang der x - Achse bewegt, trägt Energie Störungen, und nach einer Kollision mit Teilchen bewegen vorwärts, rückwärts, Energie im ungestörten Zustand der Umwelt (Figur 5 a, b) an die Energie des Teilchens entspricht.

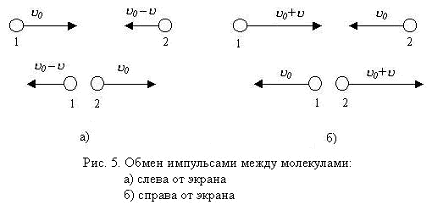
Bei einer Änderung der Bildschirmbewegung und Partikeldichte.

Unter Berücksichtigung , dass u «c, Verdickung im Bildschirm nach rechts von [3]:

In diesem Fall wird die kinetische Energie pro Volumeneinheit der Teilchen Störungsenergie in Richtung des Bildschirms unterzogen gleich:

und die kinetische Energie in der gleichen Zeit, die andere Hälfte der Partikel in die entgegengesetzte Richtung auf den Bildschirm übertragen:

Der Unterschied zwischen (7) und (8) bestimmt die Größe und Richtung der Energie, die von einer Welle der Empörung und rechts auf dem Bildschirm ausgeführt, wo die Ausbreitung von Kondensationsstoßwellenenergiedichte ist gleich:

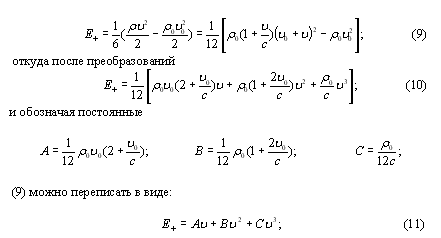
Durch ähnliche Berechnungen finden wir die Energiedichte, die durch die Verdünnungswelle auf der linken Seite des Bildschirms durchgeführt wird:

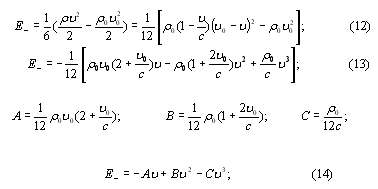
Da die Ausbreitung der Welle ändert sich die Konzentration der Teilchen in dem Medium, das heißt der durchschnittliche Abstand zwischen ihnen, dann ändern und die potentielle Energie des ausgewählten Volumens des Mediums. In der klassischen Theorie der Wellenenergie , kinetischer Energie besteht Schwingungen der Teilchen aus der Umgebung und der potentiellen Energie der elastischen Verformung des Mediums, die Dichte der kinetischen und potentiellen Energien gleich sind zu jeder Zeit und an jeder Stelle des Mediums (2) durchgeführt wird .
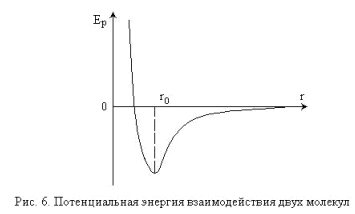
Die potentielle Energie der Wechselwirkung zwischen zwei Teilchen als Funktion des Abstands zwischen ihnen ist , um den in Figur 6 gezeigten Form. Unter normalen Bedingungen (p = 1 atm, und T = 200C, r ~ 10r0), der Abstand zwischen den Luftmolekülen r »ro, so die Ausbreitung von akustischen Wellen in einer Umgebung , in Verdünnungs potentielle Energie des Mediums zunimmt, und in der Verdickung ( im Gegensatz klassische Theorie) - reduziert. angesichts der Tatsache jedoch, daß die Gasmoleküle unter diesen Bedingungen Ek "Ep durch die potentielle Energie der Wechselwirkung der Moleküle in der Ausbreitung von akustischen Wellen in der Atmosphäre ändert, wie bei der Änderung der kinetischen Energie im Vergleich kann praktisch vernachlässigt werden, und das Gas kann als ideal betrachtet werden.

Drehzahlschwankungen Bildschirm u «c und u« u0. Dann vernachlässigen in (10) und (13) Mitglieder des Proportional U2 und U3, ganz genau können wir das im allgemeinen Fall, in Vektor - Form annehmen, die Energiedichte durch eine ebene Welle getragen:

wobei der Vektor u bestimmt den Betrag der Wellenenergie und Richtung seiner Zirkulation.
Wenn der Bildschirmoberschwingungen: x = Hsinwt und seine Geschwindigkeit u = Hw coswt, dann wird der Wert der Energiedichte durch die Welle getragen wird , unterscheidet sich grundsätzlich von den Energiewerten durch die klassische Formel [4, p.363]: Wellenenergie ist proportional der Dichte des Mediums, die Geschwindigkeit der Zufalls thermischen Molekularbewegung, die Amplitude und Frequenz, anstatt die Quadrate der Amplitude und Frequenz Schwingungsquelle.

Konstituierenden Energie proportional u2 u3 und tragen erheblich zu den Energiewerten der Welle bei hohen Frequenzen und Amplituden der Schwingungsquelle , die, während der Ausbreitung, wie Schallwellen in dem Medium führt zu nichtlinearen Effekten.

Erworbene Partikel pro Volumeneinheit des Mediums in die Ausbreitungsimpulswelle der Kondensation ist:

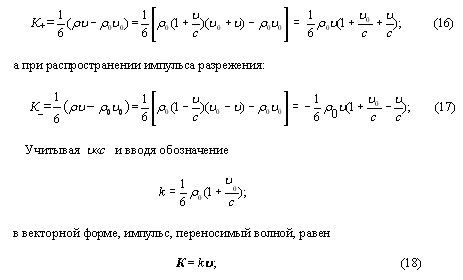
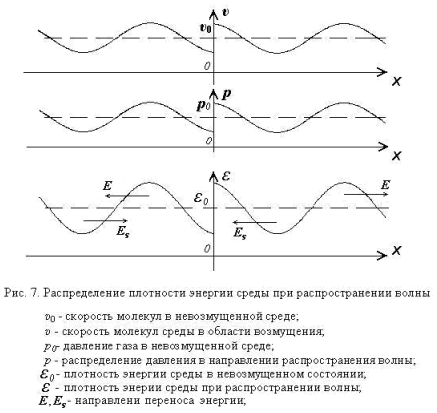
Da die Richtung des Bildschirms Geschwindigkeit u jede halbe Periode ändert, dann wird jeder Halbperiode (im Gegensatz zu der klassischen Theorie) und die Änderung der Richtung der übertragenen Welle von Impuls und Energie. Instant Verteilung der inneren Energie in dem Medium und der Richtung der Energieübertragung in der Ausbreitung einer ebenen Welle entlang der x-Achse an einem bestimmten Punkt in der Zeit sind in Abbildung 7 gezeigt , wobei E - die Richtung der Übertragung des Energiewelle , die durch die Quelle und die Richtung der Energieübertragung Es- emittiert wird , durch Umverteilung der inneren Energie des Mediums (Bildschirm am Ursprung platziert). Der Momentanwert der Energie von der Welle E (x, t) am Punkt x zum Zeitpunkt t (8) transportiert ist:

und der positive Wert von E bedeutet , dass die Richtung der Energieübertragung und der Ausbreitungs gleich sind, negativ - Energie übertragen wird (im Gegensatz zu der klassischen Theorie) in die entgegengesetzte Richtung.

In der Praxis bestimmen die Registrierung der akustischen Welle und dessen Parameter den Schalldruck, und als Empfänger der akustischen Schwingungen Mikrophone, die irgendwie verfolgen die Fluiddruckschwankung während des Durchgangs der Wellen und wandeln sie in elektrische Schwingungen und in der klassischen Physik, die Wellenintensität ist proportional zum Quadrat des Schalldrucks unter Verwendung von .
Es wird, daß der Gasdruck in der ungestörten Medium bekannt:

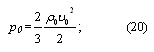
In diesem Fall wird eine Änderung der Umgebungsdruck auf der Membranmikrophon wenn der Schallwelle, die durch Veränderung der Partikeldichte und Geschwindigkeit verursacht Streuung wird aus dem Ausdruck bestimmt wird:

Feststellung, dass die eingeklammerte Menge der Energie, die durch die Welle übertragen proportional ist, schließen wir, dass die Wellenenergiedichte und bzw. und die Intensität des Schalls zu der Amplitude des Schalldrucks proportional ist, anstatt der quadratischen:

Die Ursache für diese Unterschiede ist , dass , wenn die klassische Theorie der Wellenenergie der Berechnung nicht berücksichtigt , ist die Tatsache , daß die Teilchen bereits beginnen , Geschwindigkeit und kinetische Energie vor der Störung in dem Medium (Fig. 7).

Grundsätzlich unterscheidet sich von der allgemein akzeptierte Erklärung für die Prozess- und Interferenzwellen.

In der klassischen Version, wenn in einem homogenen und isotropen Medium durch zwei kohärente Wellen in einem beliebigen Punkt im Raum angeregt werden, werden Wellen mit dem Prinzip der Überlagerung nach lagert: jeder Punkt (Molekül) des Mediums, wo die Menschen auf zwei oder mehr Wellen kommen, zugleich verursacht Teil der Schwingungen nehmen durch individuell jede Welle [2]. Um zu bestimmen , separat die Bewegung eines Teilchens ist die Bewegung der Teilchen des Mediums in jeder Welle, und dann fassen diese Bewegungen (Abbildung 1).

In dieser Ausführungsform werden zwei Teilchen, von denen jede die Störung durch zwei verschiedene Vibrationsquellen im Falle der Wechselwirkung von Austauschimpulse verursacht trägt: die erste nach der Kollision bis zur nächsten Kollision ertragen die Dynamik zu ihrem zweiten Teilchen übertragen und umgekehrt: die zweite Partikel tragen wird, die Dynamik auf sie übertragen erste, d.h. jedes Teilchen wird bei der Übertragung von Störungen von nur einer Quelle (5) beteiligt sind . Option - Interaktion, die in 1 gezeigt ist es möglich , außer im Fall der gleichzeitigen Wirkung der beiden Teilchen in die dritte, aber nach den Anfangsbedingungen, ein solches Ereignis unwahrscheinlich. Daher ist die Teilchen des Mediums, in dem das Subjekt mehreren Wellen, dem Überlagerungsprinzip inakzeptablen: jedes Teilchen in der Übertragung des Impulses und der Energie von nur einer Hand beteiligt ist, oder das gleiche: outrage aus verschiedenen Quellen zu verschiedenen Teilchen übertragen.

Folglich können wir sagen: die Interferenzwellen ausbreiten, ohne einander zu beeinflussen, die Umverteilung der Energieflüsse und andere Zusammenarbeit als Folge der Überlagerung von Wellen nicht vorhanden ist, und die Gesamtenergiedichte am Beobachtungspunkt ist gleich der Gesamtenergiedichte der störenden Wellen:

Wenn zwei Wellen mit gleichen Amplituden in der gleichen Richtung verteilt sind , an den Punkten Interferenz maximale Amplitude des Schalldrucks wird verdoppelt, und daher werden zugegeben und die Energiedichte der entstehenden Wellen (Abbildung 9). An Punkten Interferenz minimal , wenn überlagerte Bereich Verdickungseinzelwellen mit rarefaction Bereich des anderen Signals nicht festgelegt ist, wie in diesem Fall die Richtung der Übertragung von Energie und Impuls der interferierenden Wellen entgegengesetzt sind, und bei gleichen Amplituden von Oszillationen, deren kumulative Wirkung auf das Membranmikrophon Null (Fig .9b). Daher ist es durch die Wellen Zugabe, ist es notwendig, nicht nur die Menge an Energie und Impuls von der Welle getragen zu betrachten, sondern auch die Richtung ihrer Migration.

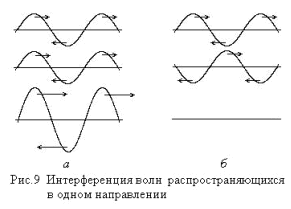
Ähnliche Prozesse treten in der stehenden Welle.

Es ist bekannt, dass, wenn zwei kohärente interferieren, die gleiche Amplitude in entgegengesetzten Richtungen bewegen, die Wellen, die sich ergebende Wellenbewegung eine stehende Welle bezeichnet wird. Die stehende Welle durch die Anwesenheit von Knotenpunkten (die Punkte Interferenzminimum) gekennzeichnet ist, die Schwingungsamplitude gleich Null ist, die mittlere Partikel an diesen Stellen nicht durch diese Punkte bewegen (nach der klassischen Ideen) gibt es keine Energieübertragung und im allgemeinen wird die Energie nicht nur entlang einer stehenden Welle, verteilte Teilchen schwingen zwischen dem Knoten und der Austausch von Energie [2].

Bei dieser Auslegung der Erklärung gemacht anders.

In der sogenannten die Knotenpunkte der Teilchen, sich kontinuierlich bewegenden, Wellenenergie in eine Richtung übertragen wird, vor der Kollision in der gleichen Richtung bewegt, mit den Teilchen, die die Energie der Welle, die sich in die entgegengesetzte Richtung transportieren. Nach der Kollision und den Austausch von Impulsen in entgegengesetzter Richtung, bis die nächste Kollision Partikel tragen in der gleichen Richtung Impulswellenausbreitungs. So ändert periodisch die Fahrtrichtung und den Austausch von Impulsen Partikel abwechselnd Energie beider Wellen tragen, so dass sie jeweils in eine andere Richtung verteilt, ohne sich gegenseitig zu beeinflussen. Mit Hilfe von Schallwellen-Empfängern, wie beispielsweise ein Mikrofon, für kleine Schwingungsamplituden, Gegenströme von Energie und Impuls durch den Knotenpunkt der stehenden Welle und der Interferenzpunkte Minimum in der Interferenz von Wellen mit gleichen Amplituden der Schwingungen können aufgrund ihrer Wirkung auf den Empfänger gleich groß erfasst werden, aber die entgegengesetzte Richtung, und das Ergebnis Null ist. Aber dennoch ist ein Interferenzminimum an den Punkten der Welle nicht "Quench" einander, und die Bedingung "anregungs dennyh 'Teilchen an den Knotenpunkten: Die Geschwindigkeit, Leistung und eine Teilchendichte unterscheidet sich von den entsprechenden Werten im ungestörten Medium.

Bis jetzt, wo die Ausbreitung von Wellen Betrachtung nicht berücksichtigt die Tatsache, dass die Partikelkollisionen führen zu einer Änderung in der Richtung der Geschwindigkeit der kollidierenden Teilchen in jedem anderen Winkel als der Anfangsrichtung der Wellenausbreitung. Als Folge dieser Abweichungen Wellenenergie wird von Partikeln getragen wird, kann in einem Winkel zur ursprünglichen Richtung erstrecken. Im Bildbereich (Wellenquelle), wobei diese Energieströme (aufgrund der chaotischen Bewegung von Molekülen und Streuprozesse bei Kollisionen) im Durchschnitt gegenseitig kompensiert, und nur an den seitlichen Begrenzungen der ebenen Welle wird Verteilung der Wellenenergie von der ursprünglichen Richtung weg beobachtet werden. Ähnliche Prozesse wird das Treffen Wellen mit einem Hindernis stattfinden, die die Ursache der Beugung von Wellen ist.

Solche Transferprozesse oder Diffusion der Schwingungsamplitude entlang der Wellenfront (über den Strahl) in der Ausbreitung der Welle beobachtet wird, wenn die Amplitude entlang der Wellenfront ändert.

Die Welle trägt, Impuls und Energie von einem Ort zu einem anderen Raum, so dass es in die Übertragung von Energie die ganze Zeit schwingen über die Gleichgewichtsposition beteiligt alle Teilchen des Mediums genommen. Aus (10), (13) und (16), (17) ist es klar, dass in der Ausbreitung von Longitudinalwellen, die Impuls und Energie in der positiven Halbwelle tolerierbaren Impuls und Energie übersteigt, die jeweils mit den Mengen, die in der negativen Halbwelle durch:

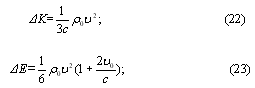
was zu der Übertragung des Mediums durch eine Schallwelle, und bei großen Amplituden führt zu einem konstanten Strom in Form von sogenannten Akustik-Streaming.

FAZIT

1. Die Energie, die von einer Welle getragen ist proportional zu der Amplitude und Frequenz der Schwingungsquelle, anstatt Quadrate.

2. Wenn die Interferenzenergie der resultierenden Oszillation ist die Summe der Energien der austretenden Wellen.

3. Die Energie, die von einer Welle der Empörung getragen wird, wird durch die Menge nicht nur aus, sondern auch die Richtung seiner Übertragung und Ausbreitung in der harmonischen Wellenumgebung wird die Übertragungsrichtung jede halbe Periode geändert.

LITERATUR

1. GS Landsberg, Optik, Nauka, Moskau (1976), S.. 88.

2. SP Gunmen, Handwerken, Nauka, Moskau (1975), S.. 481.

3. SE Haykіn, Fіzichnі Grundlagen der mehanіki, Radyans'ka Schule, Kiew (1966), s.674.

4. V.E.Kuzmichev, Gesetze und Formeln der Physik, Naukova Dumka, Kiew (1989), S.. 363.

Druckversion
Autoren: VI Stetsovich
Erscheinungsdatum 10.11.2006gg

NEUE ARTIKEL UND VERÖFFENTLICHUNGEN
	Die Technologie der Herstellung von Kardangelenken für besvarochnogo, gewinde, besflyantsevogo Verbindungsrohrsegmente in Hochdruckleitungen (ein Video)
	Erdöl und Erdölprodukte Reinigungstechnologie
	Auf die Möglichkeit aufgrund der inneren Kräfte mechanisches System von beweglichen
	Glow Flüssigkeit in einem dünnen dielektrischen kanaloh
	Die Beziehung zwischen Quanten und der klassischen Mechanik
	Millimeterwellen in der Medizin. Ein neuer Look. IIM - Therapie
	Magnetmotor
	Die Wärmequelle auf der Basis von Einheiten nososnyh