- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
Заключні зауваження
Поява вимоги цілочисловості в економічних задачах є досить очевидною і пов’язана з наявністю у моделях параметрів, які можуть набувати тільки цілих значень. Нелінійність, яка випливає з вимог цілочисловості змінних, є незначною. Тому цілочислове програмування часто розглядають як розділ математичної оптимізації лінійних моделей, в яких на деякі чи всі змінні накладено умову цілочисловості.
Зауважимо, що задачі цілочислового програмування є частковим випадком загальнішого типу задач — дискретної оптимізації. Вимоги дискретності змінних, якщо не в явному вигляді, то в прихованій формі властиві багатьом практичним типам задач, що забезпечує дуже широке коло застосування дискретного програмування в багатьох теоретичних і прикладних дисциплінах. Задачі проектування, планування, розміщення, класифікації і управління добре формалізуються за допомогою різних моделей дискретного програмування.
Особливої актуальності нині набувають проблеми вивчення ефективності методів і відповідних програмних засобів, оцінки точності розв’язків, які отримано за допомогою наближених методів, дослідження стійкості математичних моделей, побудови діалогових пакетів прикладних програм, що уможливлюють проведення досліджень в інтерактивному режимі.
Контрольні запитання
- Яка задача математичного програмування називається цілочисловою?
- Наведіть приклади економічних задач, що належать до цілочислових.
- Як геометрично можна інтерпретувати розв’язок задачі цілочислового програмування?
- Охарактеризуйте головні групи методів розв’язування задач цілочислового програмування.
- Опишіть алгоритм методу Гоморі.
- Що означає «правильне відтинання»?
- Опишіть алгоритм методу гілок та меж.
Приклади та завдання для самостійної роботи
Задача 6.1. Розв’яжіть задачі цілочислового програмування методом Гоморі.
-
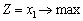 2)
2)
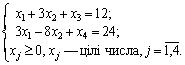

Задача 6.2. На основі умовно-оптимального плану задачі цілочислового програмування побудуйте допоміжне обмеження Гоморі і приєднайте його до останньої симплексної таблиці, знайдіть цілочислові розв’язки задачі або покажіть, що вони не існують.
Таблиця 6.8
Базис |
Сбаз |
|
–3 |
–4 |
0 |
0 |
0 |
|
|
|
|
|
|||
|
0 |
7/11 |
5/11 |
9/11 |
0 |
0 |
1 |
|
0 |
10/11 |
2/11 |
3/11 |
1 |
0 |
0 |
|
0 |
3/11 |
15/11 |
–4/11 |
0 |
1 |
0 |
|
0 |
3 |
4 |
0 |
0 |
0 |
|
Задача 6.3.Розв’яжіть задачу цілочислового програмування методом «гілок та меж»:
1) 

Created/Updated: 25.05.2018
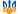 |
|








