Haupt- Andere Disziplinen Bücher Matisch mathematische programuvannya - Nakonechny S.І.

Matisch mathematische programuvannya - Nakonechny S.І.

11.5. Geometrische іnterpretatsіya gris 2 x 2

Nayprostіshim vipadkom skіnchennoї gris Je Parn gras, wenn an der Haut Teilnehmer Je Dvi strategії.

Rozglyanemo vipadok, wenn nicht sogar Gras Got sіdlovoї Punkt. Otzhe, 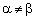. Neobhіdno wissen, dass tsіnu gris zmіshanі strategії. Poznachimo shukanі Werte ymovіrnoctey zastosuvannya "reine" Und nach strategіy gravtsya 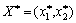Und für gravtsya B - durch .

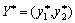Zgіdno s Hauptsatz teorії Igor, Yakscho Gravets A pritrimuєtsya svoєї optimalnoї strategії dann vigrash bude dorіvnyuvati tsіnі gris. Otzhe, Yakscho Gravets A pritrimuvatimetsya svoєї optimalnoї strategії 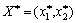, Dann gilt:

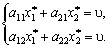(11.3)

Oskіlki 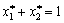dann 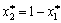. Pіdstavivshi Tsey viraz in rіvnyan System (11.3), otrimaєmo:

.

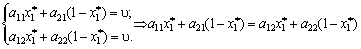Rozv'yazavshi Dana rіvnyannya vіdnosno nevіdomogo 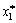, Maєmo:

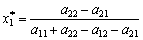(11.4)

todі: 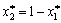= 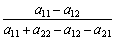. (11.5)

Provіvshi analogіchnі mіrkuvannya stosovno gravtsya B maєmo:

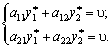(11.6)

Oskіlki 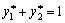dann .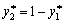

.

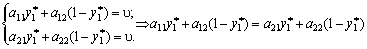Rozv'yazavshi tse rіvnyannya vіdnosno nevіdomogo 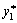, Maєmo:

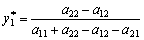(11.7)

todі: 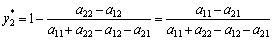. (11.8)

Tsіnu gris u znahodyat, pіdstavlyuchi Werte 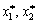(abo 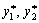In Yak), ob s rіvnyan (11.3) abo (11.6):

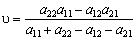. (11.9)

rozv'yazok gris s platіzhnoyu Matrix Wissen:

Rozv'yazannya. Perekonaєmosya, scho nicht gras sіdlovoї Punkt Got:

.

.

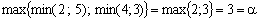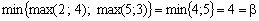Otzhe, gras tsya sіdlovoї Punkt not Got. Skoristaєmosya Formeln (11,4) (11,5) (11,7) (11,8) (11,9). Maєmo:

;

;

;

.

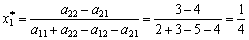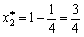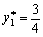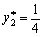Cena gris .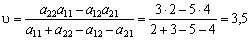

Otzhe, optimale Haut strategіya gravtsya polyagaє in der Tat Bewohner vipadkovo cherguvati svoї "chistі" strategії. Gravets Got A vikoristovuvati Perche strategіyu s іmovіrnіstyu 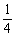Und die andere - s іmovіrnіstyu 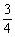Und Gravets B - navpaki. Für Tsikh Köpfen serednіy vigrash dorіvnyuvatime 3.5.

Rozv'yazku gris 2 x 2 kann dati naochnu geometrische іnterpretatsіyu.

Rozglyanemo GRU s platіzhnoyu Matrixform:

Vіdmіtimo auf osі Abszisse vіdrіzok dovzhinoyu scho dorіvnyuє odinitsі (Abb. 11.1). Lіvy kіnets vіdrіzka (Punkt h Abszisse x = 0) bude vіdpovіdati strategії A 1, und die Regeln kіnets (x = 1) - strategії A 2, OOO Alle promіzhnі Punkt tsogo vіdrіzka vіdpovіdatimut zmіshanim strategіyam gravtsya A und іmovіrnіst x 1 strategії A 1 bude dorіvnyuvati vіdstanі od Punkt P auf der rechten Seite kіntsya vіdrіzka und ymovіrnіst strategії x 2 a 2 - vіdstanі zu lіvogo kіntsya vіdrіzka. Provedemo durch den Punkt A 1 A 2 , die senkrecht zu den beiden osі Abszisse: vіs vіs das I i II. Auf pershіy sie vіdmіtimo vigrash für Vibor s strategії A 1, und drugіy - für A 2 strategії.

Nekhay Gegner VIBRAT strategіyu In 1 їy vіdpovіdayut auf den Achsen des I ist der II Dvi Punkt B 1 und dovzhina vіdrіzka A 1 1 dorіvnyuє und 11 und dovzhina vіdrіzka A 2 B 1 dorіvnyuє und 12.

Analogіchno buduєmo direkt in 2 2, Yak vіdpovіdaє strategії B 2.

Neobhіdno optimal kennen strategіyu X *, Taku, für yakoї mіnіmalny vigrash gravtsya A bude Maximum. Für tsogo vidіlimo Fett lіnієyu malyunku am unteren Rand des Köpfen Mezhuyev vigrashu Vibor strategіy In 1 In 2, die, tobto Lamans lіnіyu in 1 MB 2. tsіy mezhі znahodyatsya Werte mіnіmalnogo vigrashu gravtsya Und ob yakoї Yogo zmіshanoї strategії. Offensichtlich scho s naykrasche mozhlivih mіnіmalnih Werte in Nashomu prikladі znahoditsya in tochtsі M und zagalnomu vipadku vіdpovіdaє tіy tochtsі de Kurve, scho poznachaє mіnіmalny vigrash gravtsya A nabuvaє Maximalwert. ORDINATE tsієї Punkt Je tsіnoyu gris u. Vіdstan zu lіvogo kіntsya vіdrіzka x 2 ist das Recht auf vіdstan kіntsya vіdrіzka - 1 x dorіvnyuyut vіdpovіdno ymovіrnostyam strategіy A 2 ist die A 1.

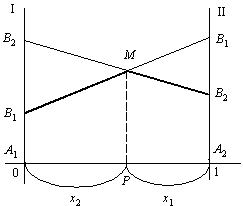
Fig. 11.1

Geometrische іnterpretatsіya daє takozh zmogu naochno zobraziti Boden , dass die obere tsіnu gris (Abb. 11.2). Für nashogo Hintern unten tsіnoyu gris vіdrіzka Je Wert von A 2 B 2 und die oberen tsіnoyu gris - A 2 B 1.

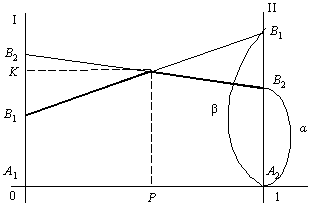
Fig. 11.2

Auf tsomu Nun Zeichnungen kann ich geometrische іnterpretatsіyu optimal strategіy Gegner B. Dіysno, chastka rozglyanuti 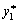strategії B1 optimalnіy zmіshanіy strategії 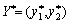dorіvnyuє vіdnoshennyu dovzhini vіdrіzka KB2 dovzhin vіdrіzkіv HF 2 HF sumi ist die 1 osі I: .

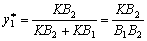W schweben mіrkuvan leicht visnovuvati scho GRU 2 x 2 kann elementarnimi priyomami rozv'yazati. Analogіchno Mauger Buti rozv'yazana gras 2 x n, tobto wenn Gravets und bekam Deprivation Dvi strategії und Gravets In - n. In diesem razі auf Figur slіd zobraziti Peretin n Zeilen, scho vіdpovіdatimut n strategіyam gravtsya aus. Mіnіmalnі vigrashі gravtsya A yavlyatimut ihn takozh Lamans lіnіyu Maximalwert yakoї i optimal für gravtsya A viznachatime strategіyu (Abb. 11.3).

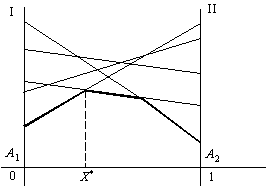
Fig. 11.3

Mozhna takozh rozv'yazati GRU i m x 2, s tієyu rіznitseyu scho neobhіdno viznachati nicht Tiefstwert vigrashu und die obere i Maximalwerte und mіnіmalne nicht mozhlivih s znahoditi.