Haupt- Wirtschaft Bücher Modelyuvannya Wirtschaft - Vіtlіnsky VV

Modelyuvannya Wirtschaft - Vіtlіnsky VV

10.2. Banken, die stochasticity modelyuvannya fіnansovih potokіv

10.2.1. Osnovnі kontseptsії stochasticity modelyuvannya fіnansovih potokіv

Yak zovnіshnі Köpfe scho vplivayut auf dіyalnіst komertsіynogo Bank (chi fіnansovoї fіrmi), so verarbeitet i scho rozvivayutsya von der Bank selbst, Yea führen skladnoї i neodnoznachnoї vzaєmodії bagatoh chinnikіv, Gründe, Brache, Bagato s yakih Got vipadkovu (ymovіrnіsnu) i / chi nechіtku (rozplivchastu) Natur. Naslіdkom tsogo Yea diejenigen scho Roboter bankіvskoї stellen die Ziffer mіroyu obtyazhena neviznachenіstyu, die ihr rizikom zumovlenim.

Ein Zi sposobіv für Relief yakogo mozhna opisati Einfädeln Mahlgefäß (chi іnshoї fіnansovoї іnstitutsії), Je Opis Yogo für Relief Eigenschaften des Vektors:

x = (x 1, ..., xn).

Kіlkіsny dass yakіsny Lager Komponente des Vektors x viznachaєtsya detalіzatsії Bühne.

Tsya sachliche Bestandsaufnahme wird die Bank für zmіstom bankіvskomu angemessenes Gleichgewicht bilden: die Komponenten des Vektors x mozhut Buti Yak іnterpretovanі zvichaynі stattі Balance und Menge їh i Struktur yogo vіdpovіdayut rіvnyu agregovanostі (schodenny - yaky vklyuchaє rahunki ein weiterer Auftrag, chi uzagalneny - Quarterly Toscho). Konkretnі kozhnoї Werte xj z - Komponente des Vektors x werden viznachayutsya obrannyam odinits vimіryuvannya für vіdpovіdnogo Ressource (Information). Zdebіlshogo tse vimіryuvachі koshtіv in tіy chi іnshіy valyutі; Buti Formgebung kann ich so zvanі resursnі odinitsі (p. Od.). Stan okremogo j-ten Ressource ototozhnyuєtsya s deyakim Elements mnozhini nevіd'єmnih dіysnih Zahlen 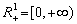Geometrische Weise yakoї Je dodatna pіvvіs dіysnoї chislovoї osі. Otzhe, Mahlgefäß zagalom mozhna Steuern deyakoyu Punkt nevіd'єmnogo Orthanten n- mіrnogo evklіdovogo Weite:

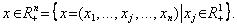
Mnozhina vsіh mozhlivih (zulässige) tochok (vektorіv) x utvoryuє Prostir stanіv Bank:

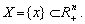
Mozhut stvoryuvatisya takozh pevnі pohіdnі (vtorinnі) Merkmale:

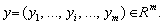
Zaznachimo scho Vektor pohіdnih Eigenschaften 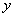Je funktsієyu od Vektor x: y = f (x) .

Yak Hintern Typen pohіdnih (vtorinnih) Eigenschaften werden Banksystem postaє obov'yazkovih fіnansovih normativіv (koefіtsієntіv), scho їh ustanovlyuyut tsentralnі Banken chi INSHI regulyuyuchі Körper.

Für vrahuvannya chinnika Stunde potrіbno zadati deyaku mnozhinu T Elements kotroї Stunde T nazivayut Momente t I. Traditsіyno Yak - Modell "neperervnogo fіzichnogo" Stunde vikoristovuyut mnozhinu tochok neskіnchennoї odnomіrnoї dіysnoї chislovoї osі R 1 von fіksovanim cob vіdlіku und mnozhina vsіh urahovuvanih momentіv Stunde T - tse Pevnyi vіdrіzok auf tsіy osі.

Yakscho gegebenes Modell neperervnogo Stunde, die Eigenschaften -ї Lager j können Yak funktsії Werte xj (t), bei scho viznachena mnozhinі T rozglyadati i nabuvaє Wert auf mnozhinі 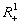. Grafіk funktsії xj (t) vіdіgraє Rolle traєktorії zmіni in Eigenschaften -ї chasі j. Stan Bank zagalom - tse Werte vektornoї funktsії Stunde:

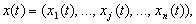(10.13)

und traєktorіya Sistemi 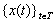Je deyakoyu Kurve (gіperpoverhneyu) in n -mіrnomu prostorі.

Viznachaєtsya TAKE ponyattya takozh, Yak "potіk".

Potіk - tse Ekonomichna Wert KOTRA vimіryuєtsya in rusі s urahuvannyam rozglyaduvanogo іntervalu Stunde. Rozmіrnіst flow - tse obsyag, podіleny auf іnterval Stunde.

Zmіstovny bіk ponyattya "potіk 's pov'yazany ponyattyam shvidkostі zmіni Lagersystem.

Yakscho pripustiti scho funktsії xj (t), scho zadayut traєktorії zmіni Merkmale werden Bank Je in allen Punkten , die diferentsіyovanimi Zugang glatt іntervalu T = (T - T +), dann vіdpovіdnі Pershi pohіdnі

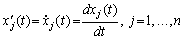(10.14)

mozhna іnterpretuvati Yak shvidkostі zmіni Tsikh Eigenschaften. Rozglyadayuchi spezifische Ressourcen otrimuyut vіdpovіdnі Vidi potokіv: fіnansovy, Penny, potіk gotіvki Toscho.

Dinamіka Bank in tsіlomu Mauger Buti beschrieben für die Linderung des Vektors der Ressourcenströme

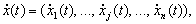
yaky zadaє Vektor shvidkostі zmіni in prostorі doslіdzhuvanogo ob'єkta wird.

Bedeutung okremoї Eigenschaften ob'єkta doslіdzhennya ob yakogo Stunde Zeit t I (T -, T + ) viznachaєtsya der Formel:

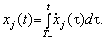(10.15)

Formuєtsya takozh Modell ґruntuєtsya Yak Yak auf vіdobrazhennі Bank-System (Vektor) Pervin Ressource potokіv:

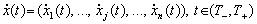. (10.16)

Analogіchno mozhna rozglyadati i pohіdnі (vtorinnі) resursnі fließt:

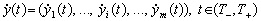. (10.17)

Obidvі s Beratungsmodelle ((10.13) , daß (10.16)) geben uyavlennya schodo Lager Bank für eine Stunde Haut Zeit t. Sie können jedoch niedrige prikladіv bringen, wenn vinikaє neobhіdnіst in perehodі od "von Punkt" eingereicht "іntegralnogo" Inventar povodzhennya j- ¯ Leistung auf Aufgaben Pevnyi іntervalі Stunde

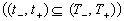. (10.18)

Für tsogo verabreicht ponyattya serednogo Eigenschaftswert (J- ¯ Vektorkomponenten werden) auf іntervalі (t -, t +):

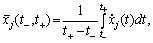(10.19)

Yak vimіryuєtsya in vіdpovіdnih Ressource odinitsyah und takozh serednogo Fluss:

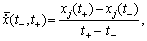(10.20)

scho vimіryuєtsya in Ressource odinitsyah auf odinitsyu Stunde. Zaznachimo scho (10,20) viznachaє serednyu shvidkіst zmіni obsyagu j- ten Ressource für іnterval (t -, t +).

Modelі dinamіki bankіvskih resursіv scho ґruntuyutsya auf neperervnomu podannі Stunden іntervalіv nicht mіroyu vіdpovіdayut Prozesse, SSMSC realіzuyutsya auf praktitsі Povny. Nach au-Perche "fіzichny Stunde" Yak Taqiy, scho i Plinius rіvnomіrno neperervno nicht zazvichay vnutrіshnіm Rhythmen "zhittєvogo Zyklus" ekonomіchnih sub'єktіv vіdpovіdaє. Klasichny Hintern nevіdpovіdnostі "fіzichnogo" i "ekonomіchnogo 's Stunde pov'yazany neobhіdnіstyu vrahuvannya vihіdnih i Svyatkovyy dnіv, uprodovzh yakih Banken tun vikonuyut nicht svoї operatsії. Alternativ neperervnіst visuvaє visokі vimogi schodo masivіv danih, neobhіdnih für vіdpovіdnogo їh testuvannya die ekspluatatsії.

Um od neperervnogo Stunde auf diskrete gehen, scho bіlsh angemessen vrahovuє Köpfen dіyalnostі fіnansovo-ekonomіchnih іnstitutіv, Mauger vikoristovuvatisya seit іntertemporalna Hіksa Modell * 3 zu kommen genannt. Zgіdno s tsієyu kontseptsієyu skіnchenny vіdrіzok Stunde [t -, t +], vprodovzh yakogo sposterіgaєtsya funktsіonuvannya doslіdzhuvanoї System podіlyaєtsya auf rіvnі K Chastain (vіdrіzki dieser napіvіntervali) dovzhinoyu d:

* 3: {Hіks J. Wert und Kapital .. - M., 1993.}

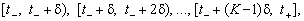
de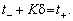

In diesem osnovі podіlu - gіpoteza für yakoyu vseredinі Tsikh іntervalіv 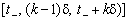usі parametrischer xj (t), scho Mühle harakterizuyut Bank , die Köpfe Yogo funktsіonuvannya, zalishayutsya (nablizheno) postіynimi i zmіnyuyutsya Deprivation in den Furchen іntervalіv Stunden. Tsya іdeya auf printsipovomu rіvnі zobrazhena in Abb. 10.1.

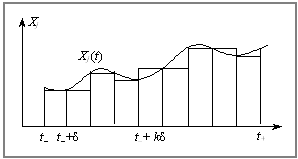
Fig. 10.1. Perehіd od neperervnogo Stunde vor in diskreten іntertemporalnіy skhemі Hіksa

Otzhe, otrimuєmo diskrete "bankіvsky" h t, Werte scho pribiraє 0,1, ..., k, ..., K. Einfache zdіysniti uzagalnennya, vrahovuyuchi diese scho Momente "bankіvskogo" t Stunde vіddіlenі promіzhkami Stunde rіznoї dovzhini. Tse dozvolyaє vrahovuvati bіlsh genau vimogu postіynostі protsesіv useredinі Tsikh vіdrіzkіv dass chinnik vihіdnih i Svyatkovyy dnіv.

Für diskrete vprovadzhennya Stunde vіdbuvaєtsya fіksatsіya vіdnosno Yogo momentіv vektorіv werden (vihіdnih Merkmale):

x (t) = (x 1 (t), ..., x j (t), ..., xn (t))

dass vektorіv Ressource potokіv:

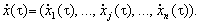
Mozhna takozh od "schodennogo" Stunde "schotizhnevogo", "schomіsyachnogo" Toscho gehen.

Krok in den folgenden protsesі vdoskonalennya rozglyaduvanogo Klasse Modelle - urahuvannya sie chinnikіv neviznachenostі dass zumovlenogo sie riziku. Für tsogo zruchno skoristatisya termіnologієyu teorії vipadkovih protsesіv. Pid vipadkovim (Stochastik) Prozess (vipadkovoyu funktsієyu Stunde) rozumіyut funktsіyu x (t), KOTRA Mauger Mutter des chi іnshu spezifischen realіzatsіyu (traєktorіyu) s deyakoї fіksovanoї mnozhini mozhlivih traєktorіy:

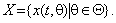
Otzhe in der Modell dinamіki neviznachenostі Köpfen wird Mauger sluguvati Vector vipadkovy Prozesse Bank:

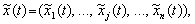
Hautkomponente 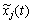yakogo opisuє stochasticity dinamіku j -ї Merkmale (Ressource) an die Bank. Analogіchno chinnik neviznachenostі, nayavny in sistemі Ressource potokіv Bank haben können opisati formalіzovanomu viglyadі for Relief Vektor vipadkovogo Prozesse:

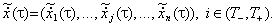
Doslіdzhennya, spryamovanі auf zmіstovny analіz zakonomіrnostey funktsіonuvannya bankіv, plagen spiratit auf danі, die i scho konkretizuyut Typ i parametrischer vikoristovuvanih vipadkovih funktsіy Werte * 4 gіpotezi.

* 4: {Hovanov NV Mathematische Modelle von Risiken und Unsicherheiten. - Sankt Petersburg, 1998}.