Teil Heim Produktion, Amateur Funkamateur Modellflugzeuge, Raketen- Nützlich, unterhaltsam	Stealth - Master Elektronik Physik der Technik Erfindung	Raum Geheimnis Erde Mysteries Secrets of the Ocean List Kartenausschnitt
Verwendung des Materials ist für die Referenz (für Websites - Hyperlinks) zulässig

DIVINE PROPORTIONEN des Goldenen Schnitts

Willkommen im Forum

Wenn Sie auf eine leere Bank kommen und auf ihm sitzen, sitzt man nicht in der Mitte der Bank (irgendwie unanständig, obwohl es einige ausgesprochen werden) und, natürlich, nicht am Rand. Wenn Sie ruhig Längenmessungen, auf dem sein Körper Sitzbank geteilt wurde, werden Sie feststellen, dass je größer das Verhältnis von Länge zu weniger gut gegen die gesamte Länge des Segments zu einem größeren und gleich etwa 1.62. Diese Zahl wird das goldene Verhältnis genannt, eine der drei berühmtesten irrationalen Zahlen, das heißt, diese Zahlen, die Dezimaldarstellung von denen unendlich und aperiodische sind. Die beiden anderen natürlich Sie wissen, ist p - Verhältnis des Umfangs zum Durchmesser und e - Basis des natürlichen Logarithmus (ein Wort, viele nicht mögen, aber die Zahl noch interessant). Und das, obwohl der goldene Schnitt und nicht das grundlegende Mathematik als eine ihrer beiden, ist es wichtig für unsere Wahrnehmung der Welt im Verhältnis zu dem Goldenen Schnitt entspricht, scheinen uns harmonisch.

Der Goldene Schnitt war den alten Griechen bekannt. Es gibt wenig Zweifel, dass einige der griechischen Architekten und Bildhauer bewusst in ihren Werken verwendet es. Ein Beispiel dafür wäre zumindest der Parthenon sein. Dieser Umstand bedeutete auch amerikanische Mathematiker Mark Barr, wenn er das Verhältnis zweier Segmente zu nennen vorgeschlagen, die goldene Verhältnis bilden, die Anzahl der j Brief (phi) - dem ersten Buchstaben im Namen des großen Phidias, der gesagt wird oft das goldene Verhältnis in seinen Skulpturen verwendet zu haben. Einer der Gründe, warum die Pythagoräer die Pentagramm gewählt haben, oder fünfzackigen Stern, ein Symbol ihrer geheimen Aufträge, ist die Tatsache, dass jeder Schnitt in der Figur ist in Gold in Bezug auf den kleinsten benachbarten Segment. Viele Mathematiker, der im Mittelalter lebte und der Renaissance waren so leidenschaftlich über das Studium der außergewöhnlichen Eigenschaften von j, war es wie ein Licht Wahnsinn.

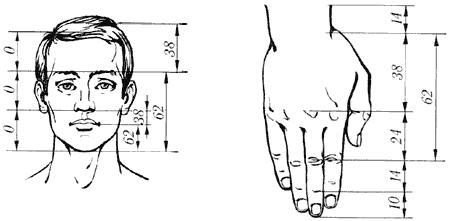
Ein Beispiel ist das Wort Kepler: "Geometrie hat zwei Schätze: eine von ihnen - den Satz des Pythagoras, die andere - die Aufteilung eines Liniensegments in extreme und mittlere Verhältnis. Die erste kann ein Maß für Gold genannt werden, die dreifache mehr wie ein Juwel ist. " In der Renaissance, durch eine Reihe j die Haltung zum Ausdruck gebracht, die so genannte "göttliche Anteil" oder nach Euklid "bedeuten und extreme Verhältnis."

Der Begriff "Goldenen Schnitt" in Gebrauch kam erst im neunzehnten Jahrhundert. Viele bemerkenswerte Eigenschaften j, manifestiert sich in einer Vielzahl von flachen und dreidimensionalen Figuren wurden im Jahr 1509 unter dem Namen «De Divina Proportione» ( «Auf der Divine Proportion") mit Illustrationen von Leonardo da Vinci in der Abhandlung Luca Pacioli, veröffentlichte gesammelt.

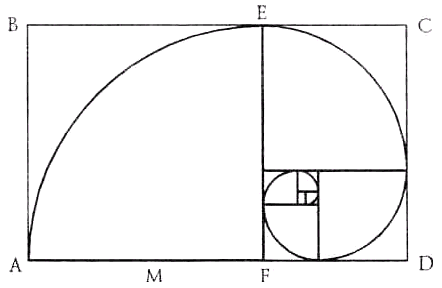
Die Zahl j drückt, beispielsweise das Verhältnis des Umfangs zu dem Radius des einbeschriebenen regulären decagon. Es gibt drei "goldene" Rechteck (dh Rechteck, dessen Seiten in der "goldenen" Verhältnis sind), so dass jeder symmetrisch mit zwei anderen (im rechten Winkel zu jedem von ihnen) gekreuzt, können wir sehen, dass die Spitze der "goldenen" Rechtecke zusammenfallen mit 12 Spitzen eines Ikosaeder und gleichzeitig zeigen die Position der Zentren der Flächen 12 regelmäßigen Dodekaeder. Goldene Rechteck hat viele ungewöhnliche Eigenschaften. Schneiden Sie aus dem goldenen Rechteck Quadrat, dessen Seite gleich der kleineren Seite des Rechtecks, so erhalten wir wieder ein goldenes Rechteck kleiner. Fortsetzung Quadrate schneiden, werden wir immer kleinere goldene Rechtecke bekommen werden. Und sie werden auf einer logarithmischen Spirale platziert werden, die in den mathematischen Modellen von natürlichen Objekten (beispielsweise Schalen von Schnecken) von großer Bedeutung ist. Spiral Pol liegt am Schnittpunkt der Diagonalen des anfänglichen Rechtecks ​​BD und der erste Schnitt vertikalen AC werden. Außerdem liegen alle nachfolgenden diagonal vermindernden goldenen Rechtecke auf dieser Diagonalen.

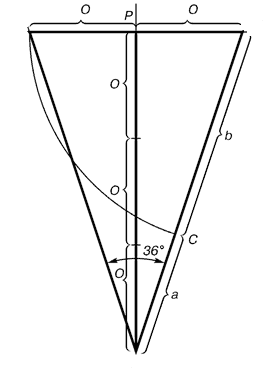
Dies ist ein gleichschenkliges Dreieck, in dem das Verhältnis der Seitenlänge gleich der Länge von 1.618 Basen. Die Pentagramm jeder der fünf Linien, diese Zahl zu komponieren, die anderen Gräben in dem Goldenen Schnitt, und die Enden der Sterne sind golden Dreiecke.

Zu allen Zeiten, Mathematik, Künstler und Philosophen wurden in Fragen beschäftigt mit dem Goldenen Schnitt bezogen. die neu "entdeckt" Allerdings, und richtet sich an Wissenschaftler und Künstler dem Goldenen Schnitt war in der Mitte des XIX Jahrhunderts präsentiert. Im Jahr 1855 veröffentlichte ein deutscher Forscher des Goldenen Schnitts Professor Zeising seine "Aesthetic Studies". Er verabsolutiert Verhältnis des Goldenen Schnitts, es universell für alle Phänomene der Natur und der Kunst zu erklären. In seiner umfangreichen (457 Seiten) arbeiten Adolf Zeising beweist, dass von allen Proportionen des goldenen Schnitts den größten künstlerischen Effekt gibt und liefert die größte Freude in der Wahrnehmung. Er verabsolutiert Verhältnis des Goldenen Schnitts, es universell für alle Phänomene der Natur und der Kunst zu erklären. Es ist in dem Goldenen Schnitt, auf Zeising, liegt der Schlüssel die gesamte Morphologie zu verstehen (einschließlich der Struktur des menschlichen Körpers), Kunst, Architektur und sogar Musik. Ein anderer deutscher Wissenschaftler Physiologe Gustav Fechner fast zu rechtfertigen versucht, sieht Zeising. Dazu maß er die Beziehung der Parteien in Tausenden von Fenstern, Bilderrahmen, Spielkarten, Bücher und andere rechteckige Gegenstände, sorgte dafür, in welcher Hinsicht Querbalken Grabkreuze auf Friedhöfen vertikalen Basis geteilt, und stellte fest, dass in den meisten Fällen hat er die Zahl erhielt etwas anders j. Fechner hat eine Reihe von ausgeklügelten Tests entwickelt, in denen Erfahrungen gefragt wurden Rechteck aus einer großen Menge von Rechtecken mit unterschiedlichen Seitenverhältnissen "zu ihm am Herzen" zu wählen, die die meisten "angenehm" Polygon zu zeichnen, einen Platz Kick wählen, usw. Und hier immer wieder durchgeführten Experimente zeigten, dass Probanden, die eine Beziehung ähnlich j bevorzugen.

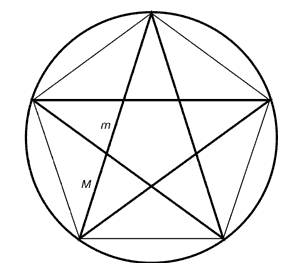
Weitere Informationen über die Geschichte des Goldenen Schnitts finden Sie unter http: //bullbear.msm/ru/rus/fr_main513.shtml Interessanter Artikel Theodore Landsheydta "Remote - Funktion des Goldenen Schnitts", in der Zeitschrift der Internationalen Gesellschaft für astrologische Forschung (ISAR) «KOSMOS» veröffentlicht. Der Autor zeichnet die Beziehung von so unterschiedlichen Phänomenen wie Schwankungen der Sonnenachse, der Anteil der Oberfläche von Dürre betroffen, Lebensmittel Termitenaktivität, die Intensität der Wirkung von Anästhetika, der Index der militärischen Aktivitäten, die Wahrscheinlichkeit für die Geburt der Jungen - und alle Schwankungen der Mengen sind in dem Goldenen Schnitt. Dr. Theodore Landsheydt ist der Direktor des Instituts für Solaraktivitätszyklen der Forschung in Kanada. Der weltbekannte Experte für solar-terrestrischen Beziehungen, erhielt er den Preis des California Institute of Zyklen in Anerkennung der herausragenden Leistungen in diesem Bereich der Forschung ausgezeichnet. Es ist besonders bemerkenswert, dass er nicht bestanden hat, und Fragmente der fraktalen Bildern der Mandelbrot-Menge, die Verknüpfung, was er dort sah, eine logarithmische Spirale fraktale chaotischen Gesetze des Universums. Lesen Sie den Artikel mag ungewöhnlich sein , auf http://astrologic.ru/library/golden.shtml

Wer will in den philosophischen Untersuchungen geknetet werden kann weitergehen http://www.radiant.ru/~kbb/Page_Gold_midl.shtml für den Artikel "Die philosophische Rechtfertigung des Begriffs der Golden Section" jedoch unserer Meinung nach , nicht besonders tief.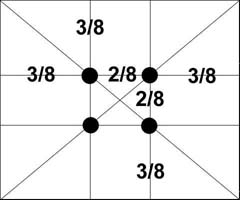

Ein interessantes Beispiel für die Verwendung des Goldenen Schnitts für eine harmonische Foto auf der Seite für Fotokunst gewidmet gezeigt www.photoline.ru/tcomp1.shtml Es basiert auf von Psychologen und Kunst Regel bemerkt - die Lage der wichtigsten Komponenten des Rahmens an den einzelnen Punkten - visuellen Zentren. Alle vier dieser Punkte, und sie sind in einem Abstand von 3/8 und 5/8 von den entsprechenden Kanten der Ebene angeordnet sind. Der Mensch hat immer konzentriert sich auf diese Punkte, unabhängig vom Format oder Frame-Bildern.

Was gleich j? Denken Sie an die Definition: ein großer Teil überhaupt auf die Mehrheit verweist. Wenn kleinere Segment als Einheit, so kann man das Verhältnis schreiben: (X + 1) / X = X / 1, die zu einem gewöhnlichen quadratische Gleichung X2-X-1 reduziert wird = 0, was die positive Wurzel ist. Diese Zahl drückt die Länge des Segments, die gleichzeitig X und den Wert von j. Seine Dezimalentwicklung ist 1.61803398 ... Wenn Sie mehr pro Einheitsintervall nehmen, wird die Länge von X durch den Kehrwert der j ausgedrückt werden, dann gibt es 1 / j. Seltsamerweise, die 1 / j = 0,61803398 ... Anzahl j - die einzige positive Zahl, die ihn in der Subtraktionseinheit im Gegenteil geht. Auch wird diese Zahl in engem Zusammenhang mit einigen metrischen Eigenschaften von regulären Polygonen und Polyedern - Fünfeck, decagon, Dodekaeder, Ikosaeder, - wie es noch 2cos (p / 5). Wie die Zahl p, j als Summe einer unendlichen Reihe in vielen Arten dargestellt werden. Maximale Leichtigkeit der folgenden zwei Beispiele unterstreicht noch einmal die grundlegende Natur von j: j j = j irrationale Zahl, kann nicht als einfacher Bruch dargestellt werden. Wenn wir jedoch die erste dieser Formeln verwenden, unsere Chance auf die erste Unterbrechung, zweiten, dritten, usw. Pluszeichen, bekommen wir eine Reihe von Fraktionen, nach und nach, die obere, der untere nähert j: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ... Wahre Liebhaber der Mathematik sicherlich bemerkt haben, dass der Nenner eine Folge von Zahlen genannt Fibonacci-Zahlen zu bilden. Jede dieser Zahlen, von der zweiten ausgehend ist die Summe der beiden vorhergehenden. Im Zähler sind zu "Zurück" Fibonacci-Zahlen. Hier ist eine der Optionen-Programm, das den Wert von j für den ersten Algorithmus berechnet, das Hinzufügen abnehm Fraktionen:

Dim Q As Double

Private Sub Form_Load ()

Öffnen Sie "c: \ qeqq.dat" für die Ausgabe als 1

Q = 1>

Für i = 1 bis 24

Q = 1 + 1 / Q

Print # 1, i, Q

Next i

End Sub

Das Programm ist in Visual Basic geschrieben, aber der gleiche Algorithmus kann in Pascal, FORTRAN, BASIC, FoxPro implementiert werden - auf jeder verfügbaren Sprache. Man beachte, dass die Variable Q als Doppel, dh mit doppelter Genauigkeit erklärt. Der springende Punkt des Algorithmus wird in der Erklärung zum Ausdruck «Q = 1 + 1 / Q», die so oft als die Seriennummer der Fraktion wird berechnet berechnet wird, alles andere ist gerahmt. Ist es nicht elegant? Das Arbeitsprogramm wird eine Tabelle:

1 2 2 1.5
3 1,66666666666667
4 1.6
5 1625
6 1,61538461538462
7 1,61904761904762
8 1,61764705882353
9 1,61818181818182
10 1,61797752808989
11 1,61805555555556
12 1,61802575107296
13 1,61803713527851
14 1,61803278688525
15 1,61803444782168
16 1,61803381340013
17 1,61803405572755
18 1,61803396316671
19 1,6180339985218
20 1,61803398501736
21 1,6180339901756
22 1,61803398820532
23 1,6180339889579
24 1,61803398867044

die zeigt, wie der Algorithmus, allmählich an die ausgewählte Nummer j verjüngt. Ebenso kann man auf die Zahl j "gewählt" und die zweite Formel, durch die Quadratwurzeln:
Dim Q As Double
Private Sub Form_Load ()
Öffnen Sie "c: \ qeqq.dat" Für Ausgabe als 1
Q = 1
Für i = 1 bis 24
Q = Sqr (1 + Q)
Print # 1, i, Q
Next i
End Sub
Das Ergebnis des Programms:

1 1,4142135623731
2 1,55377397403004
3 1,59805318247862
4 1,61184775412525
5 1,61612120650812
6 1,61744279852739
7 1,61785129060967
8 1,61797753093474
9 1,61801654223149
10 1,61802859747023
11 1,618032322752
12 1,61803347392815
13 1,61803382966122
14 1,61803393958879
15 1,61803397355828
16 1,61803398405543
17 1,61803398729922
18 1,61803398830161
19 1,61803398861137
20 1,61803398870709
21 1,61803398873667
22 1,61803398874581
23 1,61803398874863
24 1,6180339887495

Vergleich der Ergebnisse spricht zugunsten des zweiten Verfahrens wird der Wert 1.618033 Methode der Quadratwurzeln erreichte den zwölften Schritt, und das Verfahren der Summation von Fraktionen nur sechzehnten. Da wir so ernsthaft die Berechnung nahm sind, wäre es unfair, einfach die Interpretation des goldenen Schnitts als das Verhältnis von zwei aufeinander folgenden Bedingungen der Fibonacci-Reihe ignorieren. Vor allem, weil das Thema selbst Fibonacci äußerst interessant zu berechnen, weil es mit dem Konzept der Rekursion verbunden. Was ist die Funktion in allen Programmiersprachen sind (sehr kurz - es ist Teil des Programms ist genannt für einen variablen Parameter zu entwickeln). Und wenn die Funktion selbst aufruft, eine solche Technik ist Rekursion bezeichnet. In allen Lehrbüchern der Programmierung Rekursion wird durch das Beispiel der Berechnung der Fibonacci-Zahlen erklärt, und alle gängigen Artikel über diese Zahlen werden sicherlich Rekursion erwähnen. Ohne nur in den theoretischen Dschungel sagen, dass Rekursion ermöglicht es Ihnen, in Bezug auf das Volumen des Quellcodes des Programms kompakt zu schreiben. Aber im Hinblick auf die optimale Nutzung der Rekursion des Programms ist es sehr zweifelhaft. Betrachten Sie das folgende Beispiel (jetzt auf Turbo Pascal'e) berechnet die uns zu dem goldenen Verhältnis gewünscht unter Verwendung von Rekursion. Alle highlight Bestimmung in FIB-Funktionen für den ersten und den zweiten Parameterwert gleich Eins ist, und für jede aufeinanderfolgende gibt die Summe der letzten zwei Werte, und bestimmt sie, wodurch selbst!

Programm m; verwendet crt;
VAR I: INTEGER; C: CHAR; F: TEXT;
FUNKTION FIB (T: INTEGER): LONGINT;
beginnen
IF (T = 1) OR (T = 2) THEN
Fib: = 1
ELSE Fib: = FIB (T-1) + FIB (T-2)
Ende;
BEGIN
ASSIGN (F, 'C: \ QQQ.DAT');
REWRITE (F);
ClrScr;
FOR I: = 1 bis 24 DO BEGIN
WRITELN (F, I, '', FIB (I), '', FIB (i + 1), '', FIB (I + 1) / FIB (I));
END;
CLOSE (F);
C: = ReadKey;
END.

Unter Berücksichtigung der Ergebnisse des Programms, sehen wir, wie das Verhältnis der beiden benachbarten Fibonacci-Zahlen nach und nach, oben, unten, in der Nähe des Goldenen Schnitts.

1 1 1 1.0000000000E + 00
2 1 2 2.0000000000E + 00
3 2 3 1.5000000000E + 00
4 3 5 1.6666666667E + 00
5 5 8 1.6000000000E + 00
6. August 13 1.6250000000E + 00
13. Juli 21 1.6153846154E + 00
21. August 34 1.6190476190E + 00
9 34 55 00 1.6176470588E +
10 55 89 00 1.6181818182E +
11 89 144 00 1.6179775281E +
12144233 1.6180555556E + 00
13233377 1.6180257511E + 00
14377610 1.6180371353E + 00
15610987 1.6180327869E + 00
16 987 1597 1.6180344478E + 00
17 1597 2584 1.6180338134E + 00
18 2584 4181 1.6180340557E + 00
19 4181 6765 1.6180339632E + 00
20 6765 10946 1.6180339985E + 00
21 10946 17711 1.6180339850E + 00
22 17711 28657 1.6180339902E + 00
23 28657 46368 1.6180339882E + 00
24 46368 75025 1.6180339890E + 00

Der Wert von 1.618033 erschien erst am 17. Schritt, dass "schwächeren" erste Weg, aber auf der anderen Seite haben wir die Werte der 24 Mitglieder der Fibonacci-Reihe haben, und traf sich mit Rekursion. Aber das Programm funktioniert nicht optimal - Zwanzigstel des Wertes als für etwa fünf Sekunden (pIII-700 und vierzigsten als eine Minute). Zu viele "Bewegungen" hat eine rekursive Funktion, deren Zahl wie eine Lawine Zunahme der Zahl wächst, die Eleganz der Codierung zu Lasten der Leistung ging. Aber was mussten wir ein Programm machen, effektiv zu arbeiten? Stellen Sie ein Array und füllen Sie es mit der gleichen Funktion, aber ohne Rekursion, die sich auf die Anzahl der Mitglieder haben bereits gezählt, in dem Array platziert. Das Programm wird funktionieren "sofort", aber es wird nicht so schön sein.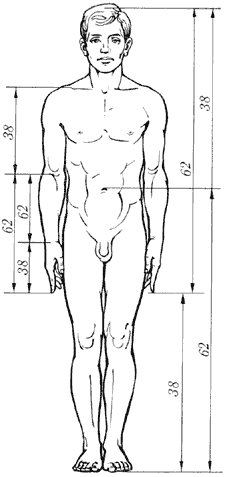

Derzeit Fibonacci Geschäftsleute und Ökonomen intensiv untersucht. Es wird bemerkt, dass die Wellen, die die Schwankungen der Wertpapierkurse sind Umschläge von kleinen Wellen, sie, die wiederum noch kleiner, und die Anzahl von kleinen Schwankungen in der Zeit beschreiben, auf eine größere Anzahl von Fibonacci entspricht. Dies war zunächst Elliott vorgeschlagen. Helson Ralph Elliott war Ingenieur. Nach einer schweren Krankheit in den frühen 1930er Jahren. er nahm die Analyse von Aktienkursen, vor allem der Dow Jones auf. Nach einer Reihe von höchst erfolgreichen Prognosen veröffentlicht Elliott eine Reihe von Artikeln im Journal of Financial World Magazine im Jahr 1939. Sie wurden zunächst seinen Standpunkt dargestellt, dass der Dow-Jones-Index Bewegung zu bestimmten Rhythmen unterliegen. Nach Elliott, alle diese Bewegungen folgen dem gleichen Recht wie die Gezeiten - die Flut Ebbe sollte, sollte die Aktion (Aktie) Zähler (Reaktion). Diese Regelung hängt nicht von der Zeit, da die Marktstruktur, als Ganzes genommen, es unverändert bleibt. Er schrieb: "Lyuboy menschliche Tätigkeit inhärent in den drei Besonderheiten: die Form, Zeit und Haltung - die alle auf die Summe der Fibonacci-Folge unterworfen sind." Wenn Sie einen Handgriff auf die Fibonacci und Elliott-Wellen-Zahlen zu erhalten, können Sie durch das Spielen an der Börse reich zu werden. Interessenten auf der Website von Elliott Wave International Internet gehen kann http://www.elliottwave.com/ die schlecht Wenn mit dem Englisch, und ich möchte , um reich zu werden - dann gehen Sie zu http://user.cityline.ru/~esfinkro/index.shtml , gibt es eine Beschreibung des Artikels über die Elliot Wave.

Das Interesse an dem Goldenen Schnitt erwärmt und periodische Ausbrüche von Popularität der Pyramiden. Zum Beispiel www.rcom.ru/tvv/Dm/str6.shtml kann unter anderen Zeichen der Pyramide von Cheops gefunden werden, und in seinen Proportionen des Goldenen Schnitts enthalten. Nicht ohne lustige Dinge zu tun. In der bereits erwähnten Seite http: //bullbear.msm/ru/rus/fr_main513.shtml finden: "Die Länge der Seiten der Pyramide von Gizeh ist 783,3 Meter (238,7 m), die Höhe der Pyramide - 484,4 ft (147,6 m). Die Länge der Fläche mit der Höhe aufgeteilt, führt zu der Beziehung P = 1,618. Die Höhe von 484,4 Meter entspricht 5.813 Zoll (08.05.13) - ist die Zahl der Fibonacci-Folge "All der Humor in der Tatsache, dass die alten Ägypter waren in Zoll kaum etwas gemessen. (Meter hier - ist eine andere Sache j) und das Aussehen der Zahlen hier Fibonacci erklärt ohne Mystik keineswegs unmöglich. Piramidostroeniem interessiert sich für moderne und ungewöhnliche Phänomene in den Pyramiden auftritt, empfehle ich den Artikel Pyramiden Enthusiasten Alexander Golod "Pyramiden in den Proportionen des Goldenen Schnitts - die Lebensdauer des Generators" befindet sich auf http://www.slavaiv.narod.ru/ . Die größte Pyramide in der Höhe von 44 Metern wurde Ende 1999 gebaut, nicht weit von Moskau auf 38 km der Autobahn von Moskau nach Riga, es ist nicht nur im Fernsehen, sprach über die Wunder in mitnimmt. Man kann nicht sagen, dass die Proportionen der Pyramide sind Gegenstand unserer Beziehungen diskutiert. Nun, das ist alles. Jetzt können Sie nicht nur intuitiv wählen das Seitenverhältnis des Palastes von Ihnen gebaut wird, sondern überprüfen sie, dem Goldenen Schnitt zu bringen. Herausforderung. Martin Gardner, Kolumnist unterhaltsam Mathematik in der Zeitschrift Scientific American, erhielt einen Brief von seinen Lesern mit der Information, dass das durchschnittliche Verhältnis des menschlichen Wachstums auf eine Höhe gleich dem Nabel j. Es wäre notwendig, um dies zu überprüfen, und Frauen können in High Heels gemessen werden. Und für die am meisten die raffinierteste Liebhaber - wie die Ergebnisse der folgenden drei Programme zu ändern, wenn die Berechnungen nicht mit einem Beginn und zum Beispiel mit einem hundert?

Druckversion
PS Material geschützt.
Erscheinungsdatum 07.03.2004gg

NEUE ARTIKEL UND VERÖFFENTLICHUNGEN
	Die Technologie der Herstellung von Kardangelenken für besvarochnogo, gewinde, besflyantsevogo Verbindungsrohrsegmente in Hochdruckleitungen (ein Video)
	Erdöl und Erdölprodukte Reinigungstechnologie
	Auf die Möglichkeit aufgrund der inneren Kräfte mechanisches System von beweglichen
	Glow Flüssigkeit in einem dünnen dielektrischen kanaloh
	Die Beziehung zwischen Quanten und der klassischen Mechanik
	Millimeterwellen in der Medizin. Ein neuer Look. IIM - Therapie
	Magnetmotor
	Die Wärmequelle auf der Basis von Einheiten nososnyh