Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

2.8.4. Розв’язування задачі лінійного програмування симплексним методом

Розглянемо, як, виходячи з початкового опорного плану задачі лінійного програмування, за допомогою симплексного методу знайти оптимальний план.

Продовжимо розгляд задачі (2.36)—(2.38), опорний план якої 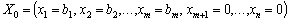. Для дослідження даного плану на оптимальність (за умовою оптимальності плану задачі лінійного програмування) необхідно вектори 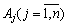системи обмежень (2.37) розкласти за базисними векторами 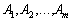і розрахувати значення оцінок .

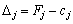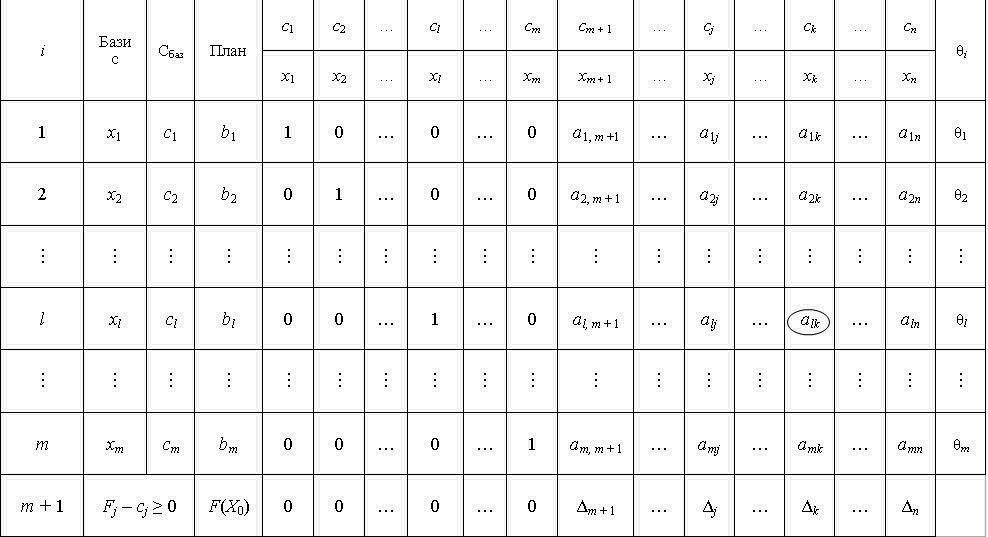
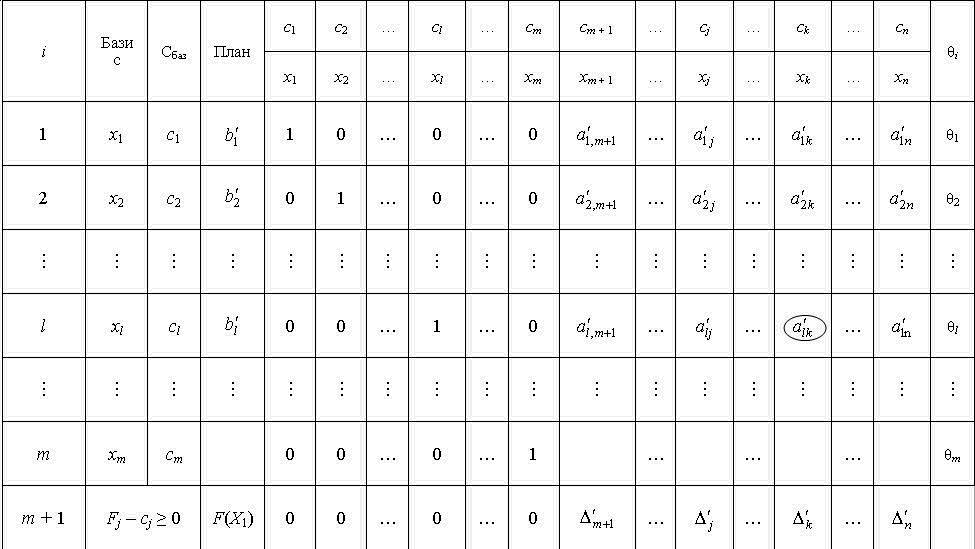
Всі подальші обчислення зручно проводити в симплексній таблиці (табл. 2.6).

У стовпці «Базис» записані змінні, що відповідають базисним векторам, а в стовпці «Сбаз» — коефіцієнти функціонала відповідних базисних векторів. У стовпці «План» — початковий опорний план 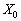, в цьому ж стовпці в результаті обчислень отримують оптимальний план. У стовпцях 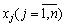записані коефіцієнти розкладу кожного j-го вектора за базисом, які відповідають у першій симплексній таблиці коефіцієнтам при змінних у системі (2.37). У (m + 1)-му рядку в стовпці «План» записують значення функціонала для початкового опорного плану 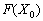, а в інших стовпцях 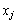— значення оцінок 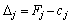. Цей рядок симплексної таблиці називають оцінковим.

Значення 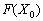знаходять підстановкою компонент опорного плану в цільову функцію, а значення 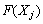— при підстановці коефіцієнтів розкладу кожного j-го вектора за векторами базису, тобто ці значення в табл. 2.6 отримують як скалярний добуток:

,

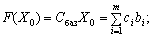
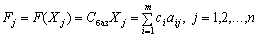де сі — коефіцієнти функціонала, що відповідають векторам базису.

Таблиця 2.6

ПЕРША СИМПЛЕКСНА ТАБЛИЦЯ ДЛЯ РОЗВ’ЯЗКУ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ

Після заповнення табл. 2.6 розраховують значення оцінок плану (останній рядок): 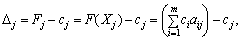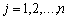. Потім згідно з умовою оптимальності плану задачі лінійного програмування, якщо всі 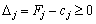(для задачі на максимум), то план є оптимальним. Допустимо, що одна з оцінок 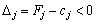, тоді план 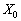не є оптимальним і необхідно здійснити перехід до наступного опорного плану, якому буде відповідати більше значення функціонала. Якщо від’ємних оцінок кілька, то включенню до базису підлягає вектор, який вибирається як 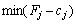. Мінімум знаходять для тих індексів j, де 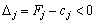. Якщо існує кілька однакових значень оцінок, що відповідають 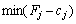, то з відповідних їм векторів до базису включають той, якому відповідає максимальне значення функціонала.

Якщо хоча б для однієї від’ємної оцінки 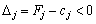всі коефіцієнти розкладу 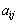відповідного вектора недодатні, то це означає, що функціонал є необмеженим на багатограннику розв’язків, тобто багатогранник у даному разі являє собою необмежену область і розв’язком задачі є .

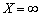Нехай 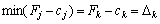, тобто мінімальне значення досягається для k-го вектора 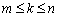. Тоді до базису включається вектор 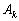. Відповідний стовпчик симплексної таблиці називають напрямним.

Для того, щоб вибрати вектор, який необхідно вивести з базису (згідно з процедурою переходу від одного опорного плану задачі до іншого — § 2.7.2), розраховують останній стовпчик табл. 2.6 — значення .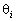

.

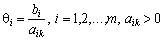З розрахованих значень необхідно вибрати найменше 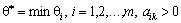. Тоді з базису виключають i-ий вектор, якому відповідає .

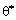Допустимо, що 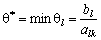відповідає вектору, що знаходиться в l-му рядку табл. 2.6. Відповідний рядок симплексної таблиці називають напрямним.

Перетином напрямного стовпчика та напрямного рядка визначається елемент симплексної таблиці alk, який називають розв’язувальним елементом. За допомогою елемента alk і методу Жордана—Гаусса розраховують нову симплексну таблицю, що визначатиме наступний опорний план задачі.

Для визначення нового опорного плану необхідно всі вектори розкласти за векторами нового базису. Вектор Аk, який необхідно вводити до базису, в розкладі за початковим базисом має вигляд:

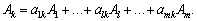(2.54)

Вектор Аl виходить з базису, і його розклад за новим базисом отримаємо з виразу (2.54):

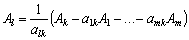. (2.55)

Розклад вектора А0 за початковим базисом має вигляд:

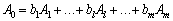. (2.56)

Для запису розкладу вектора в новому базисі підставимо вираз (2.55) у рівняння (2.56), маємо:

.

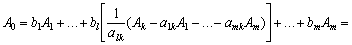
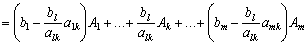Отже, значення компонент наступного опорного плану розраховуються за формулами:

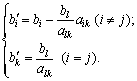(2.57)

Розклад за початковим базисом будь-якого з векторів має вигляд:

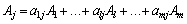. (2.58)

Розклад за новим базисом отримаємо підстановкою (2.55) у (2.58):

.

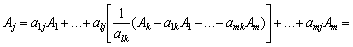
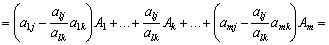
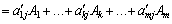Новий план: 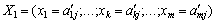, де

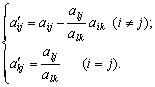(2.59)

Формули (2.57) та (2.59) є формулами повних виключень Жордана—Гаусса.

Отже, щоб отримати коефіцієнти розкладу векторів за векторами нового базису (перехід до наступного опорного плану та створення нової симплексної табл. 2.7), необхідно:

• розділити всі елементи напрямного рядка на розв’язувальний елемент;
• розрахувати всі інші елементи за формулами повних виключень Жордана—Гаусса (правило прямокутника).

Потім необхідно здійснити перевірку нових значень оцінкового рядка. Якщо всі Fj – сj ≥ 0, то план Х1 — оптимальний, інакше переходять до відшукання наступного опорного плану. Процес продовжують до отримання оптимального плану, чи встановлення факту відсутності розв’язку задачі.

Якщо в оцінковому рядку останньої симплексної таблиці оцінка Fj – сj = 0 відповідає вільній (небазисній) змінній, то це означає, що задача лінійного програмування має альтернативний оптимальний план. Отримати його можна, вибираючи розв’язувальний елемент у зазначеному стовпчику таблиці та здійснивши один крок (одну ітерацію) симплекс-методом. У результаті отримаємо новий опорний план, якому відповідає те саме значення функціонала, що і для попереднього плану, тобто функціонал досягає максимального значення в двох точках багатогранника розв’язків, а отже, за властивістю 2 (§ 2.5) розв’язків задачі лінійного програмування така задача має нескінченну множину оптимальних планів.

Таблиця 2.7

ДРУГА СИМПЛЕКСНА ТАБЛИЦЯ ДЛЯ ВІДШУКАННЯ ОПОРНОГО (ОПТИМАЛЬНОГО) ПЛАНУ

Розв’язання задачі лінійного програмування на відшукання мінімального значення функціонала відрізняється лише умовою оптимальності опорного плану. До базису включають вектор, для якого 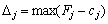, де максимум знаходять для тих j, яким відповідають 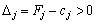. Всі інші процедури симплексного методу здійснюються аналогічно, як у задачі лінійного програмування на відшукання максимального значення функціонала.

2.8.5. Приклад розв’язування задачі симплекс-методом

Розглянемо застосування симплекс-методу для розв’язання деяких задач лінійного програмування.

Продукція чотирьох видів А, В, С і D проходить послідовну обробку на двох верстатах. Тривалість обробки одиниці продукції кожного виду наведена в табл. 2.8.

Таблиця 2.8

ТРИВАЛІСТЬ ОБРОБКИ ПРОДУКЦІЇ НА ВЕРСТАТАХ, год.

Верстат	Тривалість обробки одиниці продукції
	А	В	С	D
1	2	3	4	2
2	3	2	1	2

Витрати на виробництво одиниці продукції кожного виду визначають як величини, прямо пропорційні до часу використання верстатів (у машино-годинах). Вартість однієї машино-години становить 10 грн для верстата 1 і 15 грн — для верстата 2. Тривалість використання верстатів обмежена: для верстата 1 вона становить 450 машино-годин, а для верстата 2 — 380 машино-годин.

Ціна одиниці продукції видів А, В, С і D дорівнює відповідно 73, 70, 55 та 45 грн.

Визначити оптимальний план виробництва продукції всіх чотирьох видів, який максимізує загальний прибуток.

Побудова економіко-математичної моделі. Нехай хj — план виробництва продукції j-го виду, де j може набувати значень від 1 до 4.

Умовами задачі будуть обмеження на тривалість використання верстатів для виробництва продукції всіх видів:

для верстата 1 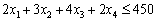(маш.-год.);

для верстата 2 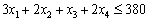(маш.-год.).

Цільовою функцією задачі є загальний прибуток від реалізації готової продукції, який розраховується як різниця між ціною та собівартістю виготовлення продукції кожного виду:

.

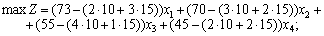
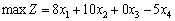Отже, математична модель цієї задачі має такий вигляд:

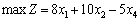
за умов:

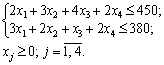
Розв’язання. Розв’яжемо задачу симплекс-методом згідно з розглянутим алгоритмом.

1. Запишемо систему обмежень задачі в канонічному вигляді. Для цього перейдемо від обмежень-нерівностей до строгих рівнянь, увівши до лівої частини обмежень додаткові змінні х5 та х6:

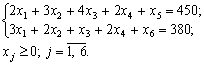
Ці додаткові змінні за економічним змістом означають недовикористаний для виробництва продукції час роботи верстатів 1 та 2. У цільовій функції Z додаткові змінні мають коефіцієнти, які дорівнюють нулю:

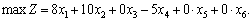
Канонічну систему обмежень задачі запишемо у векторній формі:

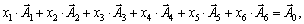
де

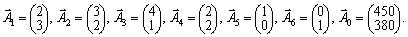
Оскільки вектори 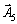та 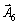одиничні та лінійно незалежні, то саме з них складається початковий базис у зазначеній системі векторів. Змінні задачі х5 та х6, що відповідають одиничним базисним векторам, називають базисними, а решту — вільними змінними задачі лінійного програмування. Прирівнюючи вільні змінні до нуля, з кожного обмеження задачі дістаємо значення базисних змінних:

Згідно з визначеними 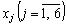векторна форма запису системи обмежень цієї задачі матиме вигляд:

.

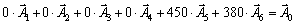Оскільки додатні коефіцієнти х5 та х6 відповідають лінійно незалежним векторам, то за означенням

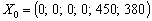
є опорним планом задачі і для цього початкового плану

.

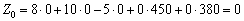2. Складемо симплексну таблицю для першого опорного плану задачі.

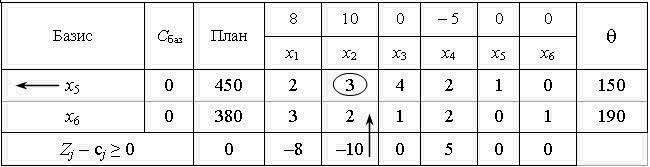
Елементи останнього рядка симплекс-таблиці є оцінками j, за допомогою яких опорний план перевіряють на оптимальність. Їх визначають так:

;

;

;

;

;

.

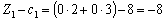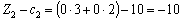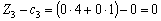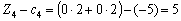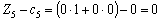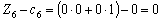У стовпчику «План» оцінкового рядка записують значення цільової функції Z, якого вона набуває для визначеного опорного плану: .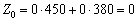

3. Після обчислення всіх оцінок опорний план перевіряють на оптимальність. Для цього продивляються елементи оцінкового рядка. Якщо всі 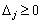(для задачі на max) або 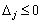(для задачі на min), то визначений опорний план є оптимальним. Якщо ж в оцінковому рядку є хоча б одна оцінка, що не задовольняє умову оптимальності (від’ємна в задачі на max або додатна в задачі на min), то опорний план є неоптимальним і його можна поліпшити.

У цій задачі в оцінковому рядку дві оцінки 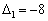та 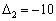від’ємні, тобто не задовольняють умову оптимальності, і тому перший визначений опорний план є неоптимальним. За алгоритмом симплекс-методу необхідно від нього перейти до іншого опорного плану задачі.

4. Перехід від одного опорного плану до іншого здійснюють зміною базису, тобто через виключення з поточного базису якоїсь змінної та включення замість неї нової з числа вільних змінних.

Для введення до нового базису вибираємо змінну х2, оскільки їй відповідає найбільша за абсолютною величиною оцінка з-поміж тих, які не задовольняють умову оптимальності (|–10|>|–8|).

Щоб визначити змінну, яка підлягає виключенню з поточного базису, для всіх додатних елементів стовпчика «х2» знаходимо відношення 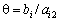і вибираємо найменше значення. Згідно з даними симплексної таблиці маємо, що 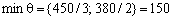, і тому з базису виключаємо змінну х5, а число а12 = 3 — розв’язувальний елемент. Дальший перехід до нового опорного плану задачі полягає в побудові наступної симплексної таблиці, елементи якої розраховують за методом Жордана—Гаусса.

Друга симплексна таблиця має такий вигляд:

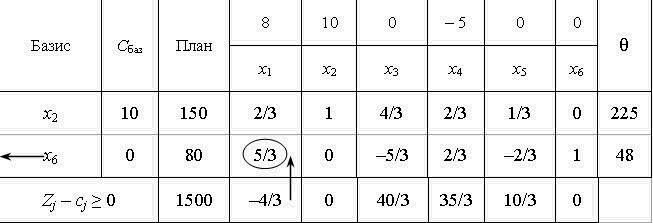
У цій таблиці спочатку заповнюють два перших стовпчики «Базис» і «Сбаз», а решту елементів нової таблиці розраховують за розглянутими нижче правилами:

1. Кожний елемент розв’язувального (напрямного) рядка необхідно поділити на розв’язувальний елемент і отримані числа записати у відповідний рядок нової симплексної таблиці.

2. Розв’язувальний стовпчик у новій таблиці записують як одиничний з одиницею замість розв’язувального елемента.

3. Якщо в напрямному рядку є нульовий елемент, то відповідний стовпчик переписують у нову симплексну таблицю без змін.

4. Якщо в напрямному стовпчику є нульовий елемент, то відповідний рядок переписують у нову таблицю без змін.

Усі інші елементи наступної симплексної таблиці розраховують за правилом прямокутника.

Щоб визначити будь-який елемент нової таблиці за цим правилом, необхідно в попередній симплексній таблиці скласти умовний прямокутник, вершини якого утворюються такими числами:

1 — розв’язувальний елемент (число 1);

2 — число, що стоїть на місці елемента нової симплексної таблиці, який ми маємо розрахувати;

3 та 4 — елементи, що розміщуються в двох інших протилежних вершинах умовного прямокутника.

Необхідний елемент нової симплекс-таблиці визначають за такою формулою:

.

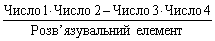Наприклад, визначимо елемент 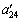, який розміщується в новій таблиці в другому рядку стовпчика «х4». Складемо умовний прямокутник:

Тоді 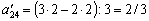. Це значення записуємо в стовпчик «х4» у другому рядку другої симплексної таблиці.

Аналогічно розраховують усі елементи нової симплексної таблиці, у тому числі й елементи стовпчика «План» та оцінкового рядка. Наявність двох способів зображення визначення оцінок опорного плану (за правилом прямокутника та за відповідною формулою) дає змогу контролювати правильність арифметичних обчислень на кожному кроці симплекс-методу.

Після заповнення нового оцінкового рядка перевіряємо виконання умови оптимальності Zj – сj ≥ 0 для другого опорного плану. Цей план також неоптимальний, оскільки 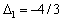. Використовуючи процедуру симплекс-методу, визначаємо третій опорний план задачі, який наведено у вигляді таблиці:

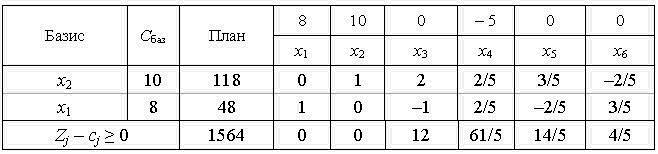
В оцінковому рядку третьої симплексної таблиці немає від’ємних чисел, тобто всі 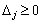і задовольняють умову оптимальності. Це означає, що знайдено оптимальний план задачі:

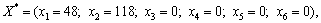
або

Х* = (48; 118; 0; 0; 0; 0);

.

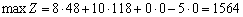Отже, план виробництва продукції, що передбачає випуск 48 одиниць продукції А та 118 одиниць продукції В, є оптимальним. Він уможливлює отримання найбільшого прибутку за заданих умов (1564 грн). При цьому час роботи верстатів використовується повністю (х5 = х6 = 0).

Наведені вище три симплексні таблиці можна об’єднати в одну та послідовно записувати в ній всі ітерації.